【题目】抛物线y=x2﹣4x+3与x轴交于A、B两点(点A在点B的左侧),点C是此抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点C在反比例函数![]() (k≠0)的图象上,求反比例函数的解析式.
(k≠0)的图象上,求反比例函数的解析式.
参考答案:
【答案】
(1)
【解答】解:令y=0,得到x2﹣4x+3=0,即(x﹣1)(x﹣3)=0,
解得:x=1或3,
则A(1,0),B(3,0),
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点C的坐标为(2,﹣1);
(2)
∵点C(2,﹣1)在反比例函数![]() (k≠0)的图象上,
(k≠0)的图象上,
∴k=﹣1×2=﹣2,
∴反比例函数的解析式为![]() ;
;
【解析】(1)令抛物线解析式中y=0得到关于x的方程,求出方程的解得到x的值,确定出A与B坐标即可;配方后求出C坐标即可;
(2)将求得的点C的坐标代入反比例函数的解析式即可求得k值.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形一共有1个平行四边形,第②个图形一共有5个平行四边形,第③个图形一共有11个平行四边形,……,则第⑥个图形中平行四边形的个数为 .

-
科目: 来源: 题型:
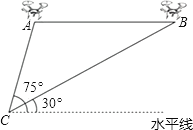
查看答案和解析>>【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是
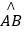 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 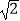 时,则阴影部分的面积为( )
时,则阴影部分的面积为( ) 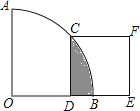
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元? -
科目: 来源: 题型:
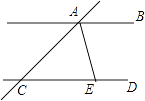
查看答案和解析>>【题目】如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
A.40°
B.70°
C.80°
D.140° -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程2x2+x﹣a=0有两个不相等的实数根,则实数a的取值范围是 .
相关试题

