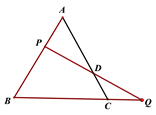
【题目】如图,△ABC中,∠A=60°,P为AB上一点, Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D, PD=DQ,证明:△ABC为等边三角形.
参考答案:
【答案】证明见解析.
【解析】试题分析:过P作PF∥BC交AC于F,得出等边三角形APF,推出AP=PF=QC,根据等腰三角形性质求出EF=AE,证△PFD≌△QCD,推出FD=CD,推出DE=![]() AC即可.
AC即可.
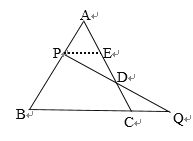
试题解析:如图,过P作PE∥BQ交AC于E,
∴∠EPD=∠Q,
在△EPD和△CQD中,
∵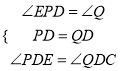
∴△EPD≌△CQD(ASA),
∴PE=CQ,∵PA=CQ,∴PE=PA,∴∠PEA=∠A=60°,
∵PE∥BQ,∴∠PEA=∠ACB=60°∴∠A=∠ACB=∠B=60°,
∴△ABC为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE中,AB=AD,AC=AE, ∠BAC=∠DAE,BC交
DE于点O,∠BAD=a.
(1)求证:∠BOD=a.
(2)若AO平分∠DAC, 求证:AC=AD.
(3)若∠C=30°,OE交AC于F,且△AOF为等腰三角形,则a= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a+a=2a2
B.(﹣a)2=﹣a2
C.(a2)3=a5
D.a3÷a=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】至少有两边相等的三角形是( )
A. 等边三角形 B. 等腰三角形 C. 等腰直角三角形 D. 锐角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣
 x+2与x轴、y轴分别交于A、B两点
x+2与x轴、y轴分别交于A、B两点(1)画出该函数的图象.
(2)求A、B两点的坐标;
(3)求直线与两坐标轴围成三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘轮船在静水中的速度是50千米/时,水流速度是a千米/时,则该轮船在逆水中航行3小时的路程为千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α、β是方程x2﹣2x﹣3=0的两个实数根,则α2﹣3α﹣αβ的值为____.
相关试题

