【题目】如图,在正方形网格中,每个小正方形的边长都为1,△ABC在网格中的位置如图所示,△ABC的三个顶点都在格点上.将点A、B、C的横坐标不变,纵坐标都乘以-1,分别得到点A1、B1、C1
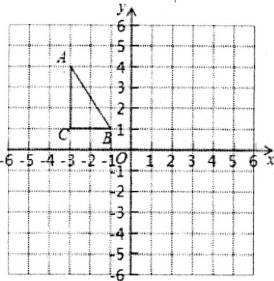
(1)写出△A1B1C1,三个顶点的坐标________;
(2)在图中画出△A1B1C1,则△ABC与△A1B1C1关于________对称;
(3)若以点A、C、P为顶点的三角形与△ABC全等,直接写出所有符合条件的点P的坐标________.
参考答案:
【答案】(1)A(-3,-4)、B(-1,-1)、C(-3,-1);(2)画图见解析,x轴; (3)(-1,4)、(-5,4)或(-5,1).
【解析】
(1)根据平面直角坐标系写出各点的坐标即可;
(2)纵坐标乘以-1变为原来的相反数,再根据网格结构找出对应点的位置,然后顺次连接即可;
(3)根据全等三角形对应边相等,分∠CAP=∠ACB=90°和∠ACP=∠ACB=90°两种情况讨论求解.
(1)A(-3,-4)、B(-1,-1)、C(-3,-1);
(2)x轴.
(3)(-1,4)、(-5,4)或(-5,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据条件求二次函数的解析式
(1)二次函数y=ax2+bx+c的对称轴为x=3,最小值为﹣2,且过(0,1)点.
(2)抛物线过(﹣1,0),(3,0),(1,﹣5)三点. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列汽车标志中,是中心对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.
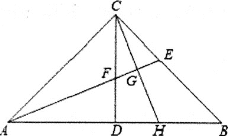
(1)直接写出∠CFE的度数________;
(2)求证:CF=BH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)3x2﹣6x+1=0(用配方法)
(2)3(x﹣1)2=x(x﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.(1)如图,若点D为线段AC的中点,求证:AD=CE;

(2)如图,若点D为线段AC上任意一点,求证:AD=CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一条排水管的截面如图所示.已知排水管的半径OB=10,水面宽AB=16.求截面圆心O到水面的距离.

相关试题

