【题目】如图,抛物线![]() 与直线
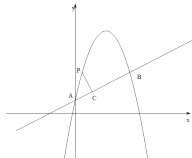
与直线![]() 交于A、B两点,其中A在y轴上,点B的横坐标为4,P为抛物线上一动点,过点P作PC垂直于AB,垂足为C.
交于A、B两点,其中A在y轴上,点B的横坐标为4,P为抛物线上一动点,过点P作PC垂直于AB,垂足为C.
(1)求抛物线的解析式;
(2)若点P在直线AB上方的抛物线上,设P的横坐标为m,用m的代数式表示线段PC的长,并求出线段PC的最大值及此时点P的坐标.
(3)若点P是抛物线上任意一点,且满足0°<∠PAB≤45°。请直接写出:
①点P的横坐标的取值范围;
②纵坐标为整数点P为“巧点”,“巧点”的个数。

参考答案:
【答案】(1)![]()
(2)![]() ,
, ![]()
(3)![]() 且
且![]() 7个.
7个.
【解析】试题分析:(1)求出A、B两点坐标代入抛物线的解析式即可解决问题.
(2)作PF⊥x轴于F,交AB于E,直线AB交x轴于D.设P(m,-m2+![]() m+1),则E(m,
m+1),则E(m, ![]() m+1),PE=-m2+4m,由△PCE∽△DOA,可得
m+1),PE=-m2+4m,由△PCE∽△DOA,可得![]() ,构建二次函数后即可解决问题.
,构建二次函数后即可解决问题.
(3)①如图2中,取点F(1,4),连接AF、FB,首先证明△FAB是等腰直角三角形,推出∠FAB=45°,设直线AF交抛物线于P,可得直线AF的解析式为y=3x+1,利用方程组求出∠PAB=45°时,点P的坐标即可解决问题,再根据对称性求出P′A⊥PA时的点P′的坐标即可解决问题.
②观察图象可知点P的纵坐标的范围3<yp≤![]() 或-
或-![]() ≤yP<3,所以整数yp为4,5,6,0,1,2,又点P的横坐标
≤yP<3,所以整数yp为4,5,6,0,1,2,又点P的横坐标![]() ≤m<4.推出对应的点P有7个,
≤m<4.推出对应的点P有7个,
试题解析:(1)由题意A(0,1),B(4,3),
把A(0,1),B(4,3)代入y=-x2+bx+c得到
![]() ,
,
解得![]() ,
,
∴抛物线的解析式为y=-x2+![]() x+1.
x+1.
(2)作PF⊥x轴于F,交AB于E,直线AB交x轴于D.
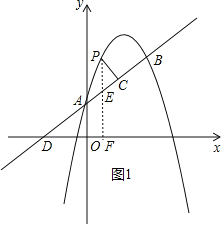
由题意D(-2,0),A(0,1),
设P(m,-m2+![]() m+1),则E(m,
m+1),则E(m, ![]() m+1),PE=-m2+4m
m+1),PE=-m2+4m
∴OA=1,OD=2,AD=![]() ,
,
∵PF∥OA,
∴∠DAO=∠DEF=∠PEC,
∵∠AOD=∠PCE=90°,
∴△PCE∽△DOA,
∴![]() ,
,
∴![]() ,
,
∴PC=-![]() (m2-4m),
(m2-4m),
∵PC=-![]() (m2-4m)=-
(m2-4m)=-![]() (m-2)2+
(m-2)2+![]() ,
,
∵-![]() <0,
<0,
∴m=2时,PC有最大值.最大值为![]() ,此时P(2,6);
,此时P(2,6);
(3)①如图2中,取点F(1,4),连接AF、FB,
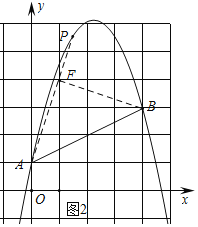
∵A(0,1),B(4,3),
∴AF=![]() ,FB=
,FB=![]() ,AB=
,AB=![]()
∴AF=FB,AF2+BF2=AB2,
∴△FAB是等腰直角三角形,
∴∠FAB=45°,设直线AF交抛物线于P,
∴直线AF的解析式为y=3x+1,
由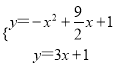
解得![]() 或
或![]() ,
,
∵A(0,1),
∴P(![]() ,
, ![]() ),
),
当P′A⊥PA时,
直线P′A的解析式为y=-![]() x+1,
x+1,
∴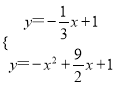 ,解得
,解得![]() 或
或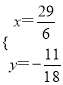 ,
,
∴P′(![]() ,-
,-![]() )
)
∴观察图象可知,满足条件0°<∠PAB≤45°的点P的横坐标![]() ≤m<4或4<m≤
≤m<4或4<m≤![]() .
.
②观察图象可知点P的纵坐标的范围3<yp≤![]() 或-
或-![]() ≤yP<3
≤yP<3
∴整数yp为4,5,6,0,1,2,又点P的横坐标![]() ≤m<4或4<m≤
≤m<4或4<m≤![]() .
.
∴对应的点P有7个,
∴“巧点”的个数为7个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,某电器商城推出了两种促销方式,且每次购买电器时只能使用其中一种方式:第一种是打折优惠,凡是在该商城购买家用电器的客户均可享受八折优惠;第二种方式是:赠送优惠券,凡在商城三天内购买家用电器的金额满400元且少于600元的,赠优惠券100元(优惠券在购买该物品时就可使用);不少于600元的,所赠优惠劵是购买电器金额的
 ,另再送50元现金.
,另再送50元现金.(1)以上两种促销方式中第二种方式,可用如下形式表达:设购买电器的金额为x(x≥400)元,优惠券金额为y元,则:①当x=500时,y= ;②当x≥600时,y= ;
(2)如果小张想一次性购买原价为x(400≤x<600)元的电器,可以使用优惠劵,在上面的两种促销方式中,试通过计算帮他确定一种比较合算的方式?
(3)如果小张在促销期间内在此商城先后两次购买电器时都得到了优惠券(两次购买均未使用优惠券),第一次购买金额在600元以内,第二次购买金额超过600元,所得优惠券金额累计达800元,设他购买电器的金额为W元,W至少应为多少?(W=支付金额-所送现金金额)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将m3(x﹣2)+m(2﹣x)分解因式的结果是
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列给出的四个命题:
①若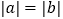 ,则
,则 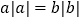 ;②若
;②若 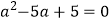 ,则
,则 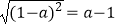 ;
;
③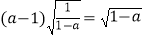 ;
;
④若方程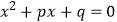 的两个实数根中有且只有一个根为0,那么
的两个实数根中有且只有一个根为0,那么 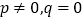 .
.
其中是真命题是( )
A.①②
B.②③
C.②④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料并解答问题:
关于勾股定理的研究有一个很重要的内容是勾股数组,在数学课本中我们已经了解到,“能够成为直角三角形三条边的三个正整数称为勾股数”,以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:
方法1:若m为奇数(m≥3),则a=m,b=
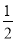 (m2﹣1)和c=
(m2﹣1)和c=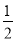 (m2+1)是勾股数.
(m2+1)是勾股数.方法2:若任取两个正整数m和n(m>n),则a=m2﹣n2,b=2mn,c=m2+n2是勾股数.
(1)在以上两种方法中任选一种,证明以a,b,c为边长的△ABC是直角三角形;
(2)某园林管理处要在一块绿地上植树,使之构成如下图所示的图案景观,该图案由四个全等的直角三角形组成,要求每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,如果每个三角形最短边上都植6棵树,且每个三角形的各边长之比为5:12:13,那么这四个直角三角形的边长共需植树 棵.
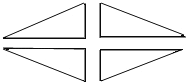
(3)某家俱市场现有大批如图所示的梯形边角余料(单位:cm),实验初中数学兴趣小组决定将其加工成等腰三角形,且方案如下:
三角形中至少有一边长为10 cm;三角形中至少有一边上的高为8 cm,
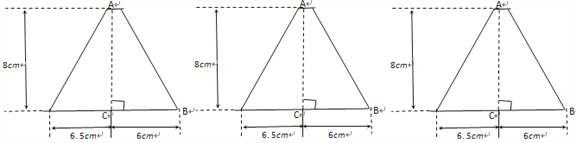
请设计出三种面积不同的方案并在图上画出分割线,求出相应图形面积.
-
科目: 来源: 题型:
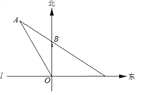
查看答案和解析>>【题目】如图,在东西方向的海岸线上有一个码头M,在码头M的正西方向有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距
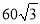 千米的A处;经过3小时,又测得该轮船位于O的正北方向,且与O相距60千米的B处.
千米的A处;经过3小时,又测得该轮船位于O的正北方向,且与O相距60千米的B处.(1)求该轮船航行的速度;
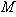 (2)当该轮船到达B处时,一艘海监船从O点出发以每小时16千米的速度向正东方向行驶,请通过计算说明哪艘船先到达码头M.(参考数据:
(2)当该轮船到达B处时,一艘海监船从O点出发以每小时16千米的速度向正东方向行驶,请通过计算说明哪艘船先到达码头M.(参考数据: 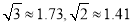 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD的对线AC、BD相交于点O,那么共得到_______个等腰直角三角形.
相关试题

