搜索
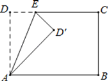
【题目】如图，长方形ABCD中，∠DAB=∠B=∠C=∠D=90°，AD=BC=6， AB=CD=10．点E为射线DC上的一个动点，△ADE与△AD′E关于直线AE对称，当△AD′B为直角三角形时，DE的长为（ ）
A.2或8B.
或18C.或2D.2或18
参考答案：
【答案】D
【解析】
分两种情况：点E在DC线段上，点E为DC延长线上的一点，进一步分析探讨得出答案即可．
解：如图1，
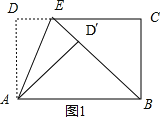
∵折叠，
∴△AD′E≌△ADE，
∴∠AD′E=∠D=90°，
∵∠AD′B=90°，
∴B、D′、E三点共线，
又∵ABD′∽△BEC，AD′=BC，
∴ABD′≌△BEC，
∴BE=AB=10，
∵
,
∴
；
如图2，
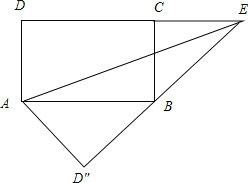
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°，
∴∠CBE=∠BAD″，
在△ABD″和△BEC中，
，
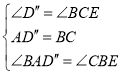∴△ABD″≌△BEC，
∴BE=AB=10，
∴DE=D″E=10+8=18．
综上所知，DE=2或18．
故答案为A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P在⊙O的直径AB的延长线上，PC为⊙O的切线，点C为切点，连接AC，过点A作PC的垂线，点D为垂足，AD交⊙O于点E．
(1)如图1，求证：∠DAC=∠PAC；
(2)如图2，点F（与点C位于直径AB两侧）在⊙O上，
，连接EF，过点F作AD的平行线交PC于点G，求证：FG=DE+DG；(3)在(2)的条件下，如图3，若AE=
DG，PO=5，求EF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知△ABC中，AB=10cm，AC=8cm，BC=6cm．如果点P由B出发沿BA方向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm/s．连接PQ，设运动的时间为t（单位：s）（0≤t≤4）．解答下列问题：
（1）当t为何值时，PQ∥BC．
（2）设△AQP面积为S（单位：cm2），当t为何值时，S取得最大值，并求出最大值．
（3）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在，求出此时t的值；若不存在，请说明理由．
（4）如图2，把△AQP沿AP翻折，得到四边形AQPQ′．那么是否存在某时刻t，使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，剪两张对边平行且宽度相等的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（ ）
A. ∠ABC=∠ADC，∠BAD=∠BCD B. AB=BC
C. AB=CD，AD=BC D. ∠DAB+∠BCD=180°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABD和△BCD都是等边三角形纸片，AB=2，将△ABD纸片翻折，使点A落在CD的中点E处，折痕为FG，点F、G分别在边AB、AD上．
（1）求证：△FBE是直角三角形；
（2）求BF的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，M、N是对角线AC上的两个动点，P是正方形四边上的任意一点，且AB=4，MN=2，设AM=x，在下列关于△PMN是等腰三角形和对应P点个数的说法中，
①当x=0（即M、A两点重合）时，P点有6个；
②当P点有8个时，x=2
﹣2；③当△PMN是等边三角形时，P点有4个；
④当0＜x＜4
﹣2时，P点最多有9个．其中结论正确的是（ ）
A. ①② B. ①③ C. ②③ D. ③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
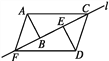
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
相关试题
