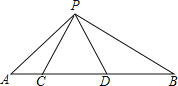
【题目】如图,点C,D在线段AB上,△PCD是等边三角形,△ACP∽△PDB,
(1)请你说明CD2=ACBD;
(2)求∠APB的度数.
参考答案:
【答案】(1)见解析;(2)∠APB=120°.
【解析】
(1)由△ACP∽△PDB,根据相似三角形的对应边成比例,可得AC:PD=PC:BD,又由△PCD是等边三角形,即可证得CD2=ACBD;
(2)由△ACP∽△PDB,根据相似三角形对应角相等,可得∠A=∠BPD,又由△PCD是等边三角形,即可求得∠APB的度数.
(1)证明:∵△ACP∽△PDB,
∴AC:PD=PC:BD,
∴PDPC=ACBD,
∵△PCD是等边三角形,
∴PC=CD=PD,
∴CD2=ACBD;
(2)解:∵△ACP∽△PDB,
∴∠A=∠BPD,
∵△PCD是等边三角形,
∴∠PCD=∠CPD=60°,
∴∠PCD=∠A+∠APC=60°,
∴∠APC+∠BPD=60°,
∴∠APB=∠APC+∠CPD+∠BPD=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC,∠ABC=120°,AC=2
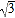 ,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )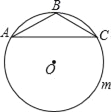
A. y=
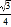 x+4 B. y=
x+4 B. y=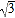 x+4 C. y=
x+4 C. y=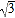 x2+4 D. y=
x2+4 D. y=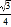 x2+4
x2+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形
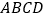 中,
中,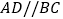 ,
,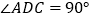 ,
,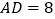 ,
,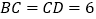 ,点
,点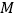 从点
从点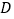 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点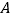 运动,同时,点
运动,同时,点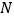 从点
从点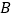 出发,以每秒1个单位长度的速度向点
出发,以每秒1个单位长度的速度向点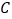 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点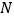 作
作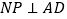 于点
于点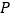 ,连接
,连接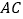 交
交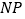 于点
于点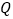 ,连接
,连接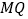 ,设运动时间为
,设运动时间为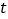 秒.
秒.(1)连接
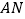 、
、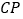 ,当
,当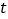 为何值时,四边形
为何值时,四边形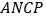 为平行四边形;
为平行四边形;(2)求出点
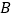 到
到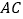 的距离;
的距离;(3)如图2,将
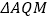 沿
沿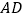 翻折,得
翻折,得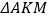 ,是否存在某时刻
,是否存在某时刻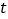 ,使四边形
,使四边形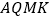 为菱形,若存在,求
为菱形,若存在,求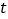 的值;若不存在,请说明理由
的值;若不存在,请说明理由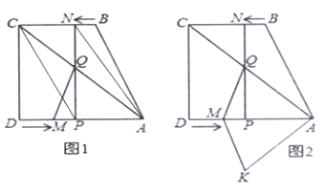
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】“双十一”已经成为中国电子商务行业的年度盛事,每年这一天成为全民的购物节.在今年的“双十 一”期间,某网店举办促销活动,方案如下表所示:
一次性购物金额
促销方案
低于
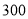 元
元所购商品全部按九折结算
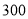 元到
元到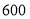 元(不包含600元)
元(不包含600元)所购商品全部按八折结算
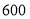 元或超过
元或超过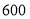 元
元其中前
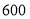 元按八折结算,超过
元按八折结算,超过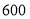 元的部分按七折结算
元的部分按七折结算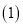 如果顾客在该网店一次性购物
如果顾客在该网店一次性购物 元(
元(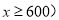 ,求实际付款多少元?(用含
,求实际付款多少元?(用含  的代数式表示)
的代数式表示)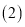 某顾客在该店两次购物的商品共计
某顾客在该店两次购物的商品共计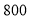 元.若第一次购物商品的金额为
元.若第一次购物商品的金额为 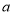 元(
元(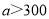 ),求该顾客两次购物的实际付款共多少元?(用含
),求该顾客两次购物的实际付款共多少元?(用含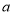 的代数式表示)
的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=﹣kx+k﹣3与直线y=kx在同一坐标系中的大致图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、E分别在△ABC的边AC和BC上,∠C=90°,DE∥AB,且3DE=2AB,AE=13,BD=9,那么AB的长为_____.

相关试题

