【题目】小明和爸爸周末步行去游泳馆游冰,爸爸先出发了一段时间后小明才出发,途中小明在离家1400米处的报亭休息了一段时间后继续按原来的速度前往游泳馆.两人离家的距离y(米)与小明所走时间x(分钟)之间的函数关系如图所示,请结合图象信息解答下列问题:
(1)小明出发 分钟后第一次与爸爸相遇;
(2)分别求出爸爸离家的距离y1和小明到达报亭前离家的距离y2与时间x之间的函数关系式;
(3)求小明在报亭休息了多长时间遇到姗姗来迟的爸爸;
(4)若游泳馆离小明家2000米,请你通过计算说明谁先到达游泳馆.

参考答案:
【答案】(1)7;(2) y1=70x+210,y2=100x;(3) 小明在报亭休息了3分钟遇到姗姗来迟的爸爸;(4) 爸爸先到达泳游馆.
【解析】
(1)根据图象得出信息解答即可;
(2)利用待定系数法即可解决问题;
(3)把y=1400代入解析式解答即可;
(4)根据题意计算解答即可.
解:(1)由图象可得:小明出发7分钟后第一次与爸爸相遇,
故答案为:7;
(2)设y1=k1x+b,
把(0,210)和(7,700)代入![]() ,
,
解得:![]() ,
,
所以解析式为y1=70x+210,
设y2=k2x,将(7,700)代入,得:700=7k2,
解得:k2=100,
所以解析式为:y2=100x;
(3)把y=1400代入y2=100x,解得:x=14,
将y=1400代入y1=70x+210,解得:x=17,
17﹣14=3,
答:小明在报亭休息了3分钟遇到姗姗来迟的爸爸;
(4)(2000﹣1400)÷100+20=26(分钟),
70×26+210=2030>2000,
答:爸爸先到达泳游馆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,到校后,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
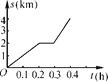
时间t/h
0
0.2
0.3
0.4
路程s/km
(3)路程s可以看成时间t的函数吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是线段AB中点,AD、BC交于点N,连接AC、BD、MC、MD,∠l=∠2,∠3=∠4.
(1)求证:△AMD≌△BMC;
(2)图中在不添加新的字母的情况下,请写出除了“△AMD≌△BMC”以外的所有全等三角形,并选出其中一对进行证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y=﹣
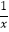 的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为 .
的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为 . 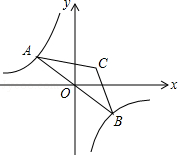
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,直线y=﹣
 x+4交坐标轴于A、B两点,过点C(﹣4,0)作CD⊥AB于D,交y轴于点E.
x+4交坐标轴于A、B两点,过点C(﹣4,0)作CD⊥AB于D,交y轴于点E.(1)求证:△COE≌△BOA;
(2)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①判断△OMN的形状.并证明;
②当△OCM和△OAN面积相等时,求点N的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校以“我最想去的社会实践地”为课题,开展了一次调查,从全校同学中随机抽取了部分同学进行调查,每位同学从“荪湖花海”、“保国寺”、“慈城古镇”、“绿色学校”中选取一项最想去的社会实践地,并将调查结果绘制成如下的统计图(部分信息未给出).
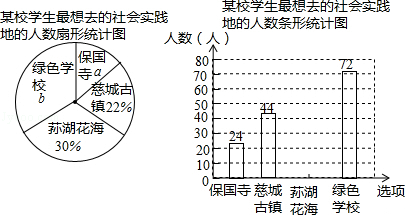
请根据统计图中信息,解答下列问题:
(1)该调查的样本容量为 , a=%,b=%,“荪湖花海”所对应扇形的圆心角度数为度.
(2)补全条形统计图;
(3)若该校共有1600名学生,请估计全校最想去“绿色学校”的学生共有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知图①中抛物线y=ax2+bx+c经过点D(﹣1,0)、C(0,﹣1)、E(1,0).
(1)求图①中抛物线的函数表达式;
(2)将图①中抛物线向上平移一个单位,再绕原点O顺时针旋转180°后得到图②中抛物线,则图②中抛物线的函数表达式为;
(3)图②中抛物线与直线y=﹣ x﹣
x﹣  相交于A、B两点(点A在点B的左侧),如图③,求点A、B的坐标,并直接写出当一次函数的值大于二次函数的值时,x的取值范围.
相交于A、B两点(点A在点B的左侧),如图③,求点A、B的坐标,并直接写出当一次函数的值大于二次函数的值时,x的取值范围. 
相关试题

