【题目】(1)已知:一次函数y=kx+b的图象经过M(0,2),(1,3)两点.求该图象与x轴交点的坐标。
(2)已知点![]() 是第一象限内的点,且
是第一象限内的点,且![]() ,点A的坐标为(10,0) .设△OAP的面积为
,点A的坐标为(10,0) .设△OAP的面积为![]() .
.
①求![]() 与
与![]() 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
②画出的图像.
参考答案:
【答案】(1)(-2,0)(2)①![]() ,
, ![]() 的取值范围是
的取值范围是![]() ②图像见解析
②图像见解析
【解析】试题分析:(1)根据待定系数法,把已知点代入函数的解析式即可得到函数的解析式,然后然后让y=0即可求出与x轴的交点;
(2)①三角形的底边是OA,高是点P的纵坐标,代入面积公式即可,并根据实际(图像在第一象限)求出x的取值范围;
②先求出与坐标轴的交点,根据两点确定一条直线作出图像,再根据自变量的取值范围取不含端点的线段即可.
试题解析:(1)由题意,得![]() 解得
解得![]() ∴k、b的值分别是1和2,
∴k、b的值分别是1和2,
∴y=x+2,∴当y=0时,x=-2,∴该图象与x轴交点为(-2,0)
(2)①∵![]() 在第一象限内,∴
在第一象限内,∴![]() ,
, ![]()
作PM⊥OA于M,则![]() . ∵
. ∵![]() ,∴
,∴ ![]()
∴![]() .即
.即![]()
![]() 的取值范围是
的取值范围是![]()
②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(﹣1,0),B(5,0)两点,与y轴交于点C(0,2)
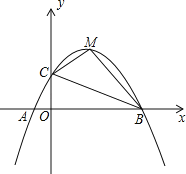
(1)求抛物线的解析式;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b是有理数,满足a<0<b,a+b>0,则把a、-a、b、-b按照从小到大的顺序排列,正确的是( )
A. -b<-a<a<b B. -b<a<-a<b C. -a<-b<a<b D. a<-b<b<-a
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种水果第一天以2元/斤的价格卖出a斤,第二天以1.5元/斤的价格卖出b斤第三天以1.2元/斤的价格卖出c斤,求:
(1)这三天一共卖出水果多少斤?
(2)这三天一共卖得多少钱?
(3)这三天平均售价是多少?并计算当a=30,b=40,c=45时,平均售价是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法将3.1416精确到0.01后,得到的近似数是____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x1,x2是一元二次方程
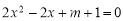 的两个实数根.
的两个实数根.(1)求实数m的取值范围;
(2)如果x1,x2满足不等式
 ,且m为整数,求m的值.
,且m为整数,求m的值. -
科目: 来源: 题型:
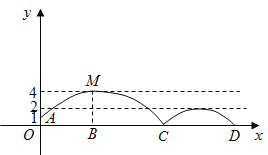
查看答案和解析>>【题目】在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在
 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 处飞出(
处飞出( 在
在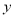 轴上),运动员孙可在距
轴上),运动员孙可在距 点6米的
点6米的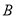 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点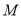 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点
 距守门员多少米?(取
距守门员多少米?(取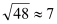 )
)(3)孙可要抢到足球第二个落地点
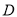 ,他应从第一次落地点
,他应从第一次落地点 再向前跑多少米?(取
再向前跑多少米?(取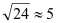 )
)
相关试题

