【题目】已知:如图,AB=AC=20,BC=32,D为BC边上一点,∠DAC=90°.求BD的长.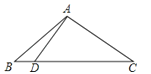
参考答案:
【答案】解:如图作AM⊥BC于M.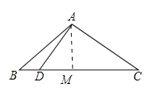
∵AB=AC=20,BC=23,AM⊥BC,
∴BM=CM=16,
∵∠C=∠C,∠AMC=∠CAD,
∴△CAM∽△CDA,
∴![]() ,
,
∴![]() ,
,
∴CD=25,
∴BD=BC﹣CD=32﹣25=7.
【解析】作AM⊥BC于M,则BM=CM=16,利用△CAM∽△CDA得![]() , 求出CD即可解决问题.
, 求出CD即可解决问题.
【考点精析】利用等腰三角形的性质和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:4a3﹣12a2+9a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2x2y)3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在对18-35岁的青年人每天发微博数量的调查中,随机抽查部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,一个人的“日均发微博条数”为m,根据调查数据整理并制作图表如下:
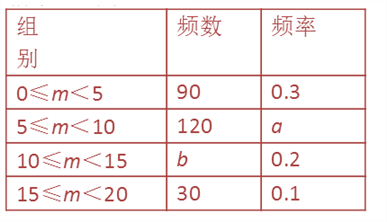
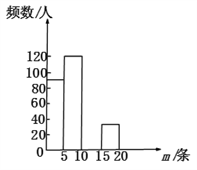
请你根据以上信息解答下列问题:
(1)在表中:a= , b=;
(2)补全频数分布直方图;
(3)若某大城市常住人口中18-35岁的青年人大约有530万人,试估计其中“日均发微博条数”不少于10条的大约有多少万人. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.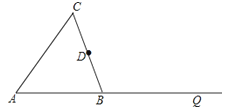
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
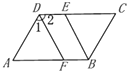
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为平行四边形ABCD的对角线AC的中点,过点O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.
(1)图中共有几对全等三角形,请把它们都写出来;
(2)求证:∠MAE=∠NCF.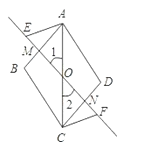
相关试题

