【题目】如图,已知点O为直线AB上一点,将一直角三角板的直角顶点放在点O处.
(1)如图1,将三角板的一边ON与射线OB重合,过点O在三角板的内部,作射线OC,使∠NOC:∠MOC=2:1,求∠AOC的度数;
(2)如图2,将三角板绕点O逆时针旋转一定角度到图2的位置,过点O在三角板MON的内部作射线OC,使得OC恰好是∠MOB对的角平分线,此时∠AOM与∠NOC满足怎样的数量关系?并说明理由.

参考答案:
【答案】(1)120°;(2)∠AOM=2∠NOC,理由见解析
【解析】
(1)根据角的倍分关系,以及角的和差关系即可求解;
(2)令∠NOC为β,∠AOM为γ,∠MOC=90°-β,根据∠AOM+∠MOC+∠BOC=180°即可得到∠AOM与∠NOC满足的数量关系.
(1)∵∠NOC:∠MOC=2:1,
∴∠MOC=90°×![]() =30°,
=30°,
∴∠AOC=∠AOM+∠MOC=90°+30°=120°.
(2)∠AOM=2∠NOC,
令∠NOC为β,∠AOM为γ,∠MOC=90°﹣β,
∵∠AOM+∠MOC+∠BOC=180°,
∴γ+90°﹣β+90°﹣β=180°,
∴γ﹣2β=0,即γ=2β,
∴∠AOM=2∠NOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“保护环境,人人有责”,为了更好的利用水资源,某污水处理厂决定购买
 、
、 两型号污水处理设备共10台,其信息如下表.(1)设购买
两型号污水处理设备共10台,其信息如下表.(1)设购买 型设备
型设备 台,所需资金共为
台,所需资金共为 万元,每月处理污水总量为
万元,每月处理污水总量为 吨,试写出
吨,试写出 与
与 之间的函数关系式,
之间的函数关系式, 与
与 之间的函数关系式;(2)经预算,该污水处理厂购买设备的资金不超过88万元, 每月处理污水总量不低于2080吨,请你列举出所有购买方案,并指出哪种方案最省钱,需多少资金?
之间的函数关系式;(2)经预算,该污水处理厂购买设备的资金不超过88万元, 每月处理污水总量不低于2080吨,请你列举出所有购买方案,并指出哪种方案最省钱,需多少资金?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小明:那直角三角形是否存在奇异三角形呢?
小红:等边三角形一定是奇异三角形.
(1)根据“奇异三角形”的定义,小红得出命题:“等边三角形一定是奇异三角形”,则小红提出的命题是 .(填“真命题”或“假命题”)
(2)若
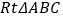 是奇异三角形,其中两边的长分别为
是奇异三角形,其中两边的长分别为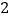 、
、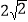 ,则第三边的长为 .
,则第三边的长为 .(3)如图,
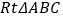 中,
中,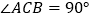 ,以
,以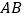 为斜边作等腰直角三角形
为斜边作等腰直角三角形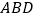 ,点
,点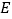 是
是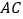 上方的一点,且满足
上方的一点,且满足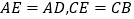 .求证:
.求证: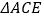 是奇异三角形.
是奇异三角形.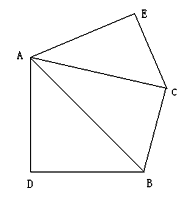
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题

(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=4 .
.
①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面各小题括号里的数,均是它前面的方程的解的是( )
A. 3x﹣1=5(2) B.
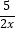 +1=0(﹣5,﹣7)
+1=0(﹣5,﹣7)C. x2﹣3x=4(4,1) D. x(x﹣2)(x+4)=0(2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(甲),在正方形
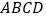 中,
中,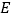 是
是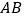 上一点,
上一点,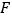 是
是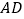 延长线上一点,且
延长线上一点,且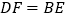 .
.(1)求证:
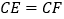 ;
;(2)在如图(甲)中,若
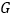 在
在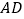 上,且
上,且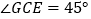 ,则
,则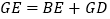 成立吗?
成立吗?证明你的结论.(3)运用(1)(2)解答中积累的经验和知识,完成下题:
如图(乙)四边形
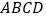 中,
中,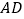 ∥
∥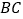 (
(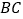 >
>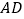 ),
),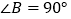 ,
,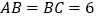 ,点
,点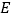 是
是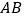 上一点,且
上一点,且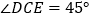 ,
,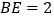 ,求
,求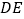 的长.
的长.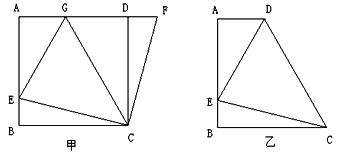
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).请解答下列问题:
(1)如果购买乒乓球
 (
( 不小于5)盒,则在甲店购买需付款 元,在乙店购买需付款 元。(用
不小于5)盒,则在甲店购买需付款 元,在乙店购买需付款 元。(用 的代数式表示)
的代数式表示)(2)当购买乒乓球多少盒时,在两店购买付款一样?
(3)如果给你450元,让你选择一家商店去办这件事,你打算去哪家商店购买?为什么?
相关试题

