搜索
【题目】已知在平面直角坐标系中，二次函数 y=x2+2x+2k﹣2 的图象与 x 轴有两个交点．
（1）求 k 的取值范围；
（2）当 k 取正整数时，请你写出二次函数 y=x2+2x+2k﹣2 的表达式，并求出此二次函数图象与 x 轴的两个交点坐标．
参考答案：
【答案】（1）k＜
；（2）（﹣2，0）和（0,0）.
【解析】
（1）根据抛物线与x轴有两个交点，求出
，即可求出k的取值范围；
（2）结合（1）中的k的取值范围得到k=1，即抛物线解析式为
，由
求得二次函数图象与x轴的两个交点横坐标．
解：（1）∵图象与x轴有两个交点，
∴方程
有两个不相等的实数根，
∴
即
解得 
（2）∵k 为正整数，
∴k=1．
∴
令 y=0，得 
解得 
∴交点为（﹣2，0）和（0，0）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是一座人行天桥的示意图，天桥的高度是10米，CB⊥DB，坡面AC的倾斜角为45°．为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面DC的坡度为i=
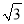：3．若新坡角下需留3米宽的人行道，问离原坡角（A点处）10米的建筑物是否需要拆除？（参考数据： 
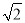≈1.414， 
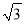≈1.732）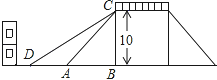
-
科目： 来源： 题型：
查看答案和解析>>【题目】（3分）在同一平面直角坐标系中，函数y=ax2+bx与y=bx+a的图象可能是（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（－3，2），B（0，4），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△
C；平移△ABC，若A的对应点
的坐标为（0，4），画出平移后对应的△
；（2）若将△
C绕某一点旋转可以得到△，请直接写出旋转中心的坐标；（3）在
轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标． -
科目： 来源： 题型：
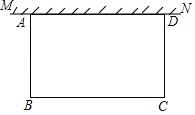
查看答案和解析>>【题目】如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．
（1）若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；
（2）求矩形菜园ABCD面积的最大值．
-
科目： 来源： 题型：
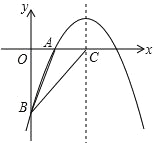
查看答案和解析>>【题目】如图，二次函数 y=﹣x2+bx+c 的图象经过 A（1，0），B（0，﹣3）两点．
（1）求这个抛物线的解析式及顶点坐标；
（2）设该二次函数的对称轴与 x 轴交于点 C，连接 BA、BC，求△ABC 的面积．
（3）在抛物线的对称轴上是否存在一点 P，使得 O、B、C、P 四点为顶点的四边形是平行四边形？若存在，请直接写出 P 点坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以△ABC的边BC为直径的⊙O交AC于点D，过点D作⊙O的切线交AB于点E．
（1）如图1，若∠ABC=90°，求证：OE∥AC；
（2）如图2，已知AB=AC，若sin∠ADE=
， 求tanA的值．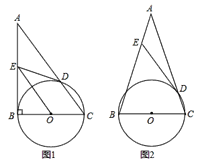
相关试题
