【题目】某人从A城出发,前往距离A城30千米的B城.现在有三种方案供他选择:
①骑自行车,其速度为15千米/时;
②蹬三轮车,其速度为10千米/时;
③骑摩托车,其速度为40千米/时.
(1)选择哪种方式能使他从A城到达B城的时间不超过2小时?请说明理由;
(2)设此人在行进途中离B城的距离为s(千米),行进时间为t(时),就(1)所选定的方案,试写出s与t之间的函数关系式(注明自变量t的取值范围),并在如图所示的平面直角坐标系中画出函数的图象.

参考答案:
【答案】(1)此人骑自行车或摩托车从A城到B城的时间都不超过2小时,理由见解析;(2)详见解析.
【解析】
(1)分别求出时间比较一下即可,时间=路程÷速度.
(2)根据题意解析式中的k与速度有关,b就是30,然后用两点法画出图象.
(1)因为30÷15=2(时),30÷10=3(时),30÷40=![]() (时),所以此人骑自行车或摩托车从A城到B城的时间都不超过2小时.
(时),所以此人骑自行车或摩托车从A城到B城的时间都不超过2小时.
(2)若骑自行车,则s=-15t+30(0≤t≤2);①
若骑摩托车,则s=-40t+30(0≤t≤![]() ).②
).②
图象如图所示: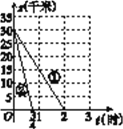
-
科目: 来源: 题型:
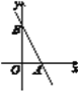
查看答案和解析>>【题目】如图,已知直线y=-2x+6与x轴交于点A,与y轴交于点B.
(1)点A的坐标为________,点B的坐标为________.
(2)求△AOB的面积.
(3)直线AB上是否存在一点C(点C与点B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司市场营销部的营销员的个人月收入y(元)与该营销员每月的销售量x(万件)成一次函数关系,其图象如图11所示.根据图象提供的信息,解答下列问题:
(1)求出营销员的个人月收入y(元)与该营销员每月的销售量x(万件)(x≥0)之间的函数关系式;
(2)已知该公司营销员李平5月份的销售量为1.2万件,求李平5月份的收入.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中画出直线y=
 x+1的图象,并根据图象回答下列问题:
x+1的图象,并根据图象回答下列问题:(1)写出直线与x轴、y轴的交点坐标;
(2)求出直线与坐标轴围成的三角形的面积;
(3)若直线y=kx+b与直线y=
 x+1关于y轴对称,求k,b的值.
x+1关于y轴对称,求k,b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料并解决有关问题:
我们知道:|x|=
 .现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别为|x+1|与|x﹣2|的零点值).在实数范围内,零点值x=﹣1和,x=2可将全体实数分成不重复且不遗漏的如下3种情况:①x<﹣1;②﹣1≤x<2;③x≥2.
从而化简代数式|x+1|+|x﹣2|可分以下3种情况:
①当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②当﹣1≤x<2时,原式=x+1﹣(x﹣2)=3;
③当x≥2时,原式=x+1+x﹣2=2x﹣1.综上讨论,原式=
 .
.通过以上阅读,请你解决以下问题:
(1)化简代数式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
 (其中
(其中 均为整数),则有
均为整数),则有 .
.∴
 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
当
 均为正整数时,若
均为正整数时,若 ,用含m、n的式子分别表示
,用含m、n的式子分别表示 ,得
,得 = ,
= , = ;
= ;(2)利用所探索的结论,找一组正整数
 ,填空: + =( +
,填空: + =( +  )2;
)2;(3)若
 ,且
,且 均为正整数,求
均为正整数,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】当x=m和x=n(m≠n)时,二次函数y=x2﹣2x+3的函数值相等,当x=m+n时,函数y=x2﹣2x+3的值为 .
相关试题

