搜索
【题目】如图，在△ABC 中，∠C=90°，∠A=34°，D，E 分别为 AB，AC 上一点，将△BCD，△ADE 沿 CD，DE 翻折，点 A，B 恰好重合于点 P 处，则∠ACP=_______________．
参考答案：
【答案】22°
【解析】
根据折叠的性质即可得到 AD=PD=BD，根据 D 是 AB 的中点，可得CD= 
AB=AD=BD，根据∠ACD=∠A=34°，∠BCD=∠B=56°，即可得出∠BCP=2∠BCD= 112°，即可得出∠ACP=112°﹣90°=22°．
由折叠可得，AD=PD=BD，
∴D 是 AB 的中点，
∴CD=AB=AD=BD，
∴∠ACD=∠A=34°，∠BCD=∠B=56°，
∴∠BCP=2∠BCD=112°，
∴∠ACP=112°﹣90°=22°.
故答案为：22°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程：
已知：直线l和l外一点P．（如图1）
求作：直线l的垂线，使它经过点P．
作法：如图2
（1）在直线l上任取两点A，B；
（2）分别以点A，B为圆心，AP，BP长为半径作弧，两弧相交于点Q；
（3）作直线PQ．
所以直线PQ就是所求的垂线．
请回答：该作图的依据是_________________________________________．
-
科目： 来源： 题型：
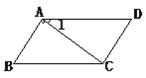
查看答案和解析>>【题目】如图，已知∠1＝30°，∠B＝60°，AB⊥AC。
（1）计算：∠DAB＋∠B
（2）AB与CD平行吗？AD与BC平行吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了锻炼学生身体素质，训练定向越野技能，某校在一公园内举行定向越野挑战赛．路线图如图1所示，点E为矩形ABCD边AD的中点，在矩形ABCD的四个顶点处都有定位仪，可监测运动员的越野进程，其中一位运动员P从点B出发，沿着B﹣E﹣D的路线匀速行进，到达点D．设运动员P的运动时间为t，到监测点的距离为y．现有y与t的函数关系的图象大致如图2所示，则这一信息的来源监测点为（ ）
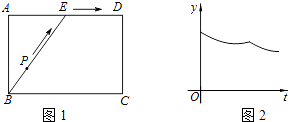
A.A点
B.B点
C.C点
D.D点 -
科目： 来源： 题型：
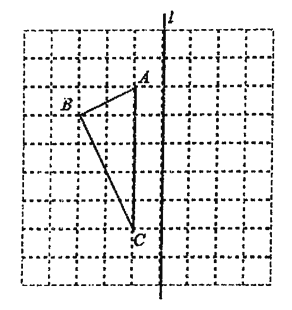
查看答案和解析>>【题目】如图，正方形网格中每个小正方形边长都是1．
(1)画出△ABC关于直线1对称的图形△A1BlCl;
(2)在直线l上找一点P，使PB=PC;（要求在直线1上标出点P的位置）
(3)连接PA、PC，计算四边形PABC的面积．
-
科目： 来源： 题型：
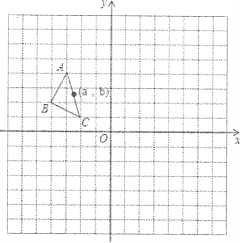
查看答案和解析>>【题目】如图，在平面直角坐标系中，AABC的三个顶点坐标为A(一3，4)，B(一4，2)，C(一2，1)，ΔABC绕原点顺时针旋转90°，得到△A1B1C1，ΔA1B1C1向左平移2个单位，再向下平移5个单位得到△A2B2C2．
(1)画出ΔA1B1Cl和△A2B2C2
(2)P(a，b)是AABC的AC边上一点，ΔABC经旋转、平移后点P的对应点分别为P1、P2，请写出点P1、P2的坐标．
-
科目： 来源： 题型：
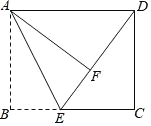
查看答案和解析>>【题目】如图，在长方形 ABCD 中，AB=8，AD=10，点 E 为 BC 上一点，将△ABE 沿 AE 折叠，使点 B 落在长方形内点 F 处， 且 DF=6，求 BE 的长．
相关试题
