【题目】（10分）如图1，在正方形ABCD中，E、F分别是边AD、DC上的点，且AF⊥BE．

（1）求证：AF=BE；

（2）如图2，在正方形ABCD中，M、N、P、Q分别是边AB、BC、CD、DA上的点，且MP⊥NQ．MP与NQ是否相等？并说明理由．

参考答案：

【答案】（1）证明：如图（1），在正方形ABCD中，AB＝DA，∠BAE＝∠D＝90°，

∴∠DAF＋∠BAF＝90°，

∵AF⊥BE，∴∠ABE＋∠BAF＝90°，∴∠ABE＝∠DAF，

∵在△ABE和△DAF中，

∴△ABE≌△DAF（ASA），∴BE＝AF．

（2）解：MP与NQ相等．理由如下：

如图（2），过点A作AF∥MP交CD于F，过点B作BE∥NQ交AD于E，则BE＝NQ，AF＝MP．只需证BE＝AF即可．与（1）的情况完全相同．

【解析】试题分析：（1）要证明AF=BE成立，只需要根据条件证明△ABE≌△DAF即可；（2）过点A作AF∥MP交CD于F，过点B作BE∥NQ交AD于E，将问题转化为证明AF=BE，即可应用（1）的结论．

试题解析：（1）证明：在正方形ABCD中，AB=AD，∠BAE=∠D=90°，

∴∠DAF+∠BAF=90°，∵AF⊥BE，∴∠ABE+∠BAF=90°，

∴∠ABE=∠DAF，∵在△ABE和△DAF中，

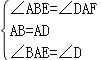，∴△ABE≌△DAF（ASA），∴AF=BE；

（2）解：MP与NQ相等．

理由如下：如图，过点A作AF∥MP交CD于F，过点B作BE∥NQ交AD于E，

由（1）可知MP＝NQ．

关闭