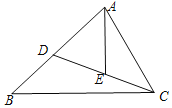
【题目】已知:如图,在△ABC中,点D在边AB上,点E在线段CD上,且∠ACD=∠B=∠BAE.
(1)求证:![]() ;
;
(2)当点E为CD中点时,求证:![]() .
.
参考答案:
【答案】(1)证明见解析,(2)证明见解析..
【解析】
(1)欲证明![]() ,只要证明△AED∽△BAC即可解决问题;
,只要证明△AED∽△BAC即可解决问题;
(2)由△DAE∽△DCA,推出![]() ,由DE=EC,可得
,由DE=EC,可得![]() ,推出
,推出![]() ,再证明AD2=ADAB即可解决问题;
,再证明AD2=ADAB即可解决问题;
(1)∵∠ACD=∠B=∠BAE,∠BAC=∠BAE+∠CAE,∠AED=∠ACD+∠CAE,
∴∠AED=△BAC,
∵∠DAE=∠B,
∴△AED∽△BAC,
∴![]() .
.
(2)∵∠ADE=∠CDA,∠DAE=∠ACD,
∴△DAE∽△DCA,
∴![]() ,
,
∵DE=EC,
∴![]() ,
,
∴![]() ,
,
∵∠DAC=∠BAC,∠ACD=∠B,
∴△ACD∽△ABC,
∴AC2=ADAB,
∴![]() .
.
-
科目: 来源: 题型:
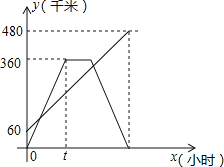
查看答案和解析>>【题目】甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出乙车出发多长时间两车相距120千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在
 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
-
科目: 来源: 题型:
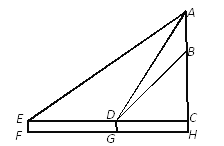
查看答案和解析>>【题目】某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
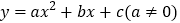 与y轴交于点C(0,2),它的顶点为D(1,m),且
与y轴交于点C(0,2),它的顶点为D(1,m),且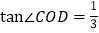 .
.(1)求m的值及抛物线的表达式;
(2)将此抛物线向上平移后与x轴正半轴交于点A,与y轴交于点B,且OA=OB.若点A是由原抛物线上的点E平移所得,求点E的坐标;
(3)在(2)的条件下,点P是抛物线对称轴上的一点(位于x轴上方),且∠APB=45°.求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:梯形ABCD中,AD//BC,AB⊥BC,AD=3,AB=6,DF⊥DC分别交射线AB、射线CB于点E、F.
(1)当点E为边AB的中点时(如图1),求BC的长;
(2)当点E在边AB上时(如图2),联结CE,试问:∠DCE的大小是否确定?若确定,请求出∠DCE的正切值;若不确定,则设AE=x,∠DCE的正切值为y,请求出y关于x的函数解析式,并写出定义域;
(3)当△AEF的面积为3时,求△DCE的面积.
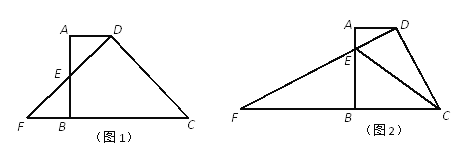
-
科目: 来源: 题型:
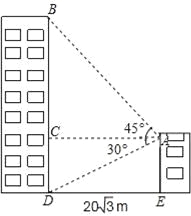
查看答案和解析>>【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20
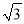 米.
米.(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
相关试题

