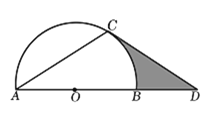
【题目】如图,点![]() 在
在![]() 直径
直径![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 上,且AC=CD,∠ACD=120°.
上,且AC=CD,∠ACD=120°.
(1)求证: ![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.
参考答案:
【答案】(1)证明见解析;(2)2![]()
![]() .
.
【解析】试题分析:(1)连接OC.只需证明∠OCD=90°.根据等腰三角形的性质即可证明;
(2)阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积.
试题解析:(1)证明:连接OC.

∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=180°-∠A-∠D-∠2=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)∵∠A=30°,
∴∠1=2∠A=60°.
∴S扇形BOC=![]() .
.
在Rt△OCD中,
∵![]() =tan60°,
=tan60°,
∴CD=2![]() .
.
∴SRt△OCD=![]() OC×CD=
OC×CD=![]() ×2×2
×2×2![]() =2
=2![]() .
.
∴图中阴影部分的面积为:2![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数的两个平方根的和是__________,商是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场试销一种成本为50元/件的
 恤.经试销发现,销售量
恤.经试销发现,销售量 (件)与销售单价
(件)与销售单价 (元/件)符合一次函数关系,试销数据如下表:
(元/件)符合一次函数关系,试销数据如下表:售价(元/件)
……
55
60
70
……
销量(件)
……
75
70
60
……
(1)求一次函数
 的表达式;
的表达式;(2)若该商场获得利润为W元,试写出利润W与销售单价
 之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式;销售单价定为多少时,商场可获得最大利润,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据3,4,x,6,8的平均数是5,则这组数据的众数是( )
A.3B.4C.6D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据2,3,2,4,2,5,3的中位数是__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣3,﹣3),B(﹣2,﹣1),C(﹣1.﹣2)是坐标平面上三点.
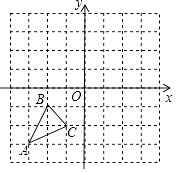
(1)写出点C关于y轴的对称点C′的坐标;
(2)画出将△ABC先向上平移5个单位,再向右平移3个单位后所对应的△A1B1C1 . 并写出△A1B1C1的各顶点坐标;
(3)将点C′向上平移a个单位后,点C′恰好落在△A1B1C1内,请你写出符合条件的一个整数a.(直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料: 解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,又∵x>1,∴y+2>1,即y>﹣1
又y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组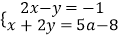 的解都为非负数.
的解都为非负数.
(1)求a的取值范围;
(2)已知2a﹣b=1,且,求a+b的取值范围;
(3)已知a﹣b=m(m是大于1的常数),且b≤1,求2a+b最大值.(用含m的代数式表示)
相关试题

