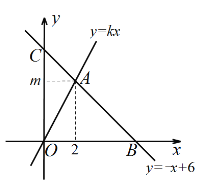
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象与正比例函数
的图象与正比例函数![]() 的图象交于点A(2,m),一次函数
的图象交于点A(2,m),一次函数![]() 的图象分别与x轴、y轴交于B、C两点.
的图象分别与x轴、y轴交于B、C两点.
(1)求m、k的值;
(2)求∠ACO的度数和线段AB的长.
参考答案:
【答案】(1)m=4,k=2;(2)∠ACO=45°,AB![]() .
.
【解析】
(1)将点A(2,m)代入y=-x+6可得m的值,再将所得点A坐标代入y=kx可得k;
(2)先求得点B、C的坐标,从而得出△OBC是等腰直角三角形,据此知∠ACO=45°,根据勾股定理可得AB的长.
解:(1)把A(2,m)代入y=-x+6得:m=-2+6=4,
把A(2,4)代入y=kx得4=2k,解得k=2;
(2)由y=-x+6可得B(6,0)、C(0,6),
∴OB=OC=6,
∴△OBC是等腰直角三角形,
∴∠ACO=45°.
设AD⊥x轴于点D,AE⊥y轴于点E,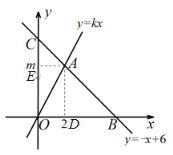
则AD=4,BD=OB-OD=6-2=4,
在Rt△ABD中,
AB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个四边形花坛ABCD,被两条线段MN, EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1、S2、S3、S4,若MN∥AB∥DC,EF∥DA∥CB,则有( )

A.S1= S4B.S1 + S4 = S2 + S3C.S1 + S3 = S2 + S4D.S1·S4 = S2·S3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
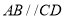 .点C在点
.点C在点 的右侧,
的右侧,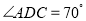 ,
,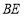 平分么
平分么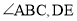 ,平分
,平分 所在的直线交于点
所在的直线交于点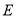 ,点
,点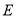 在
在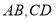 之间。
之间。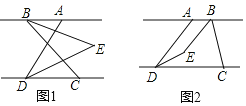
(1)如图1,点
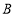 在点A的左侧,若
在点A的左侧,若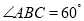 ,求
,求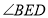 的度数?
的度数?(2)如图2,点
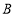 在点A的右侧,若
在点A的右侧,若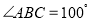 ,直接写出
,直接写出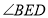 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市中学生举行足球联赛,共赛了17轮(即每队均需参赛17场),记分办法是胜-场得3分。平场得1分,负一场得0分.
(1)在这次足球赛中,若小虎足球队踢平场数与踢负场数相同,共积16分,求该队胜了几场;
(2)在这次足球赛中,若小虎足球队总积分仍为16分,且踢平场数是踢负场数的整数倍,试推算小虎足球队踢负场数的情况有几种,
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂准备用图甲所示的A型正方形板材和B型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
 若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?
若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只? 若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?
若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完? 若该工厂新购得65张规格为
若该工厂新购得65张规格为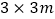 的C型正方形板材,将其全部切割成A型或B型板材
的C型正方形板材,将其全部切割成A型或B型板材 不计损耗
不计损耗 ,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共______只
,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共______只

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号以每小时16海里的速度向北偏东40°方向航行,“海天”号以每小时12海里的速度向北偏西一定的角度的航向行驶,它们离港口一个半小时后分别位于Q、R处,且相距30海里(即RQ=30).解答下列问题:
(1)求PR、PQ的值;
(2)求“海天”号航行的方向.(即求北偏西多少度?)

-
科目: 来源: 题型:
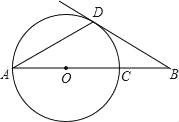
查看答案和解析>>【题目】如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=DB,∠B=30°,若⊙O的半径为4.
(1)求证:BD是⊙O的切线;
(2)求CB的长.
相关试题

