【题目】如图,已知![]() .点C在点
.点C在点![]() 的右侧,
的右侧,![]() ,
,![]() 平分么
平分么![]() ,平分
,平分![]() 所在的直线交于点
所在的直线交于点![]() ,点
,点![]() 在
在![]() 之间。
之间。
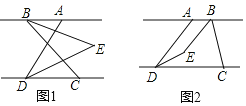
(1)如图1,点![]() 在点A的左侧,若
在点A的左侧,若![]() ,求
,求![]() 的度数?
的度数?
(2)如图2,点![]() 在点A的右侧,若
在点A的右侧,若![]() ,直接写出
,直接写出![]() 的大小.
的大小.
参考答案:
【答案】(1)![]() ;(2)
;(2) ![]() .
.
【解析】
(1)由图可知过E作AB的平行线可证得![]() =∠ABE+∠EDC,再根据角平分线可得∠ABE=30°,∠EDC=35°,即可求得
=∠ABE+∠EDC,再根据角平分线可得∠ABE=30°,∠EDC=35°,即可求得![]() =65°
=65°
(2)延长BE交DC于F,由平行可得∠ABF=∠BFC=50°,∠BFC为三角形DEF的外角,所以∠BFC=∠EDF+∠DEF,可得∠DEF=15°,可得∠BED=165°
解:(1)如图:![]() 作
作![]()

![]()
![]() ,
,
![]() 平分
平分![]() 平分
平分![]()

(2)延长BE交DC于F,

![]() 平分
平分![]() 平分∠ADC,∠ABC=100°,∠ADC=70°
平分∠ADC,∠ABC=100°,∠ADC=70°
∴∠ABE=![]() ∠ABC=50°,∠EDF=
∠ABC=50°,∠EDF=![]() ∠ADC=35°
∠ADC=35°
∵AB∥CD
∴∠ABF=∠BFC=50°
又∵∠BFC为三角形DEF的外角
∴∠BFC=∠EDF+∠DEF
∴∠DEF=15°
∴∠BED=180°-∠DEF =165°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为
 .
.(1)试求袋中绿球的个数;
(2)第1次从袋中任意摸出1球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,诵读经典”活动,学习随机抽查了部分学生,对他们每天的课外阅读时间进行调查,并将调查统计的结果分为四类:每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟记为B类,40分钟<t≤60分钟记为C类,t>60分钟记为D类,收集的数据绘制如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)这次共抽取了 名学生进行调查统计,扇形统计图中D类所对应的扇形圆心角大小为 ;
(2)将条形统计图补充完整;
(3)如果该校共有2000名学生,请你估计该校C类学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个四边形花坛ABCD,被两条线段MN, EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1、S2、S3、S4,若MN∥AB∥DC,EF∥DA∥CB,则有( )

A.S1= S4B.S1 + S4 = S2 + S3C.S1 + S3 = S2 + S4D.S1·S4 = S2·S3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市中学生举行足球联赛,共赛了17轮(即每队均需参赛17场),记分办法是胜-场得3分。平场得1分,负一场得0分.
(1)在这次足球赛中,若小虎足球队踢平场数与踢负场数相同,共积16分,求该队胜了几场;
(2)在这次足球赛中,若小虎足球队总积分仍为16分,且踢平场数是踢负场数的整数倍,试推算小虎足球队踢负场数的情况有几种,
-
科目: 来源: 题型:
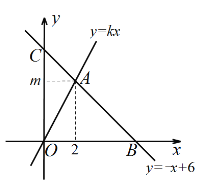
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数
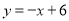 的图象与正比例函数
的图象与正比例函数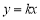 的图象交于点A(2,m),一次函数
的图象交于点A(2,m),一次函数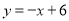 的图象分别与x轴、y轴交于B、C两点.
的图象分别与x轴、y轴交于B、C两点.(1)求m、k的值;
(2)求∠ACO的度数和线段AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂准备用图甲所示的A型正方形板材和B型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
 若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?
若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只? 若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?
若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完? 若该工厂新购得65张规格为
若该工厂新购得65张规格为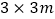 的C型正方形板材,将其全部切割成A型或B型板材
的C型正方形板材,将其全部切割成A型或B型板材 不计损耗
不计损耗 ,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共______只
,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共______只

相关试题

