【题目】(1)计算:(15x3y+10x2y﹣5xy2)÷5xy
(2)计算:(3x+y)(x+2y)﹣3x(x+2y)
(3)先化简,再求值:(x+2)(x﹣2)﹣(x+1)2,其中x=![]() .
.
参考答案:
【答案】(1) xy+2y2 (2) ﹣6
【解析】试题分析:(1)利用多项式除以单项式的运算法则计算即可;(2)利用多项式乘以多项式的运算法则、单项式乘以多项式的运算法则分别计算后,再合并同类项即可;(3)根据平方差公式和完全平方公式计算后,合并同类项,再代入求值即可.
试题解析:
(1)(15x3y+10x2y﹣5xy2)÷5xy
=3x2+2x﹣y;
(2)(3x+y)(x+2y)﹣3x(x+2y)
=3x2+6xy+xy+2y2﹣3x2﹣6xy
=xy+2y2;
(3)(x+2)(x﹣2)﹣(x+1)2
=x2﹣4﹣x2﹣2x﹣1
=﹣2x﹣5,
当x=![]() 时,原式=﹣2×
时,原式=﹣2×![]() ﹣5=﹣1﹣5=﹣6.
﹣5=﹣1﹣5=﹣6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有许多代数恒等式可以用图形的面积来表示,如图
 ,它表示了
,它表示了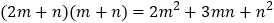
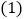 图
图 是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形
是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形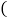 图
图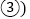 ,则图
,则图 中的阴影部分的正方形的边长等于______
中的阴影部分的正方形的边长等于______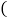 用含m、n的代数式表示
用含m、n的代数式表示
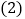 请用两种不同的方法列代数式表示图
请用两种不同的方法列代数式表示图 中阴影部分的面积.
中阴影部分的面积.方法
 ______方法
______方法 ______
______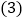 请你观察图形
请你观察图形 ,写出三个代数式
,写出三个代数式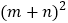 、
、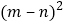 、mn关系的等式:______;
、mn关系的等式:______;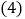 根据
根据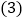 题中的等量关系,解决如下问题:若已知
题中的等量关系,解决如下问题:若已知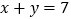 ,
,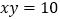 ,则
,则 ______;
______;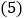 小明用8个一样大的长方形
小明用8个一样大的长方形 长acm,宽
长acm,宽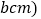 拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞
拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞 则
则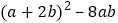 的值为______.
的值为______.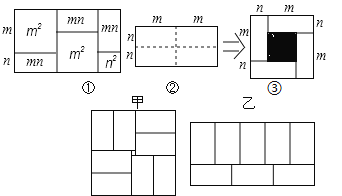
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起
 其中,
其中, ,
, ;
; :
: 若
若 ,则
,则 的度数为______;
的度数为______; 若
若 ,求
,求 的度数;
的度数; 由
由 猜想
猜想 与
与 的数量关系,并说明理由.
的数量关系,并说明理由. 当
当 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出 角度所有可能的值
角度所有可能的值 不必说明理由
不必说明理由 ,若不存在,请说明理由.
,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
(2)若∠ACD=15°,求∠AEB的度数;
(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC的平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用36000元购进甲、乙两种商品,销售完后共获利6000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5
 千米的地方有一居民点B,A、B的直线距离是10
千米的地方有一居民点B,A、B的直线距离是10  千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
千米.一天,居民点B着火,消防员受命欲前往救火.若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.) 
相关试题

