【题目】如图,直线y=kx+3与x轴,y轴分别交于A,B两点,tan∠OAB= ![]() ,点C(x,y)是直线y=kx+3上与A,B不重合的动点.
,点C(x,y)是直线y=kx+3上与A,B不重合的动点.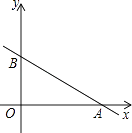
(1)求直线y=kx+3的解析式;
(2)当点C运动到什么位置时△AOC的面积是6;
(3)过点C的另一直线CD与y轴相交于D点,是否存在点C使△BCD与△AOB相似,且△BCD的面积是△AOB的面积的 ![]() ?若存在,请求出点C的坐标;若不存在,请说明理由.
?若存在,请求出点C的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵直线y=kx+3与y轴分别交于B点,
∴B(0,3),
∵tan∠OAB= ![]() ,
,
∴OA=4,
∴A(4,0),
∵直线y=kx+3过A(4,0),
∴4k+3=0,
∴k=﹣ ![]() ,
,
∴直线的解析式为:y=﹣ ![]() x+3
x+3
(2)
解:∵A(4,0),
∴AO=4,
∵△AOC的面积是6,
∴△AOC的高为:3,
∴C点的纵坐标为3,
∵直线的解析式为:y=﹣ ![]() x+3,
x+3,
∴3=﹣ ![]() x+3,
x+3,
x=0,
∴点C运动到B点时,△AOC的面积是6(C是与A、B不重合的动点,所以不符合题意);
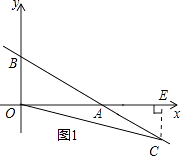
如图1,当C点移动到x轴下方时,作CE⊥x轴于点E,
∵△AOC的面积是6,
∴ ![]() EC×AO=6,
EC×AO=6,
解得:EC=3,
∴C点纵坐标为:﹣3,
∴C点横坐标为:﹣3=﹣ ![]() x+3,
x+3,
∴x=8,
∴点C点坐标为(8,﹣3)时,△AOC的面积是6
(3)
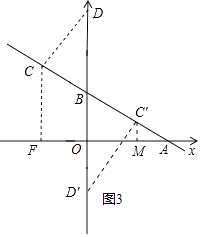
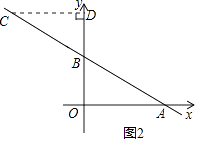
解:①如图2,当CD⊥y轴于点D时,△BCD∽△BAO,
∵△BCD的面积是△AOB的面积的 ![]() ,
,
∴相似比= ![]() ,∴BD=
,∴BD= ![]() BO=1.5,CD=
BO=1.5,CD= ![]() OA=2,
OA=2,
∴C(﹣2,4.5);
②当CD⊥y轴于点D时,△BCD∽△BAO,
∵△BCD的面积是△AOB的面积的 ![]() ,
,
∴相似比= ![]() ,∴BD=
,∴BD= ![]() BO=1.5,CD=
BO=1.5,CD= ![]() OA=2,
OA=2,
∴C点坐标为:(2,1.5);
③当CD⊥AB时,△BDC∽△BAO,
∵△BCD的面积是△AOB的面积的 ![]() ,
,
∴相似比= ![]() ,
,
∴BC=1.5,AC=6.5,
过C作CF⊥OA,
则OB∥CF,
∴CF=3.9,FA=5.2,
∴OF=1.2,
∴C(﹣1.2,3.9);
④当DC⊥AB于点C,△BCD∽△BAO,作CM⊥x轴,
当CB=1.5,BD=2.5,
∴BO∥C′M,
则有OM=1.2,C′M=2.1,
∴C(1.2,2.1).
【解析】(1)根据直线y=kx+3与y轴分别交于B点,以及tan∠OAB= ![]() ,即可得出A点坐标,从而得出一次函数的解析式;(2)根据△AOC的面积是6,得出三角形的高,即可求出C点的坐标;(3)利用△BCD与△AOB相似,利用C点不同位置,得出3种不同图形,进而利用相似,得出C点横、纵坐标,进而得出C点坐标.
,即可得出A点坐标,从而得出一次函数的解析式;(2)根据△AOC的面积是6,得出三角形的高,即可求出C点的坐标;(3)利用△BCD与△AOB相似,利用C点不同位置,得出3种不同图形,进而利用相似,得出C点横、纵坐标,进而得出C点坐标.
【考点精析】解答此题的关键在于理解一次函数的性质的相关知识,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小,以及对一次函数的图象和性质的理解,了解一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形中,
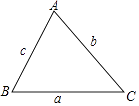
(1)猜想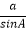 ,
, 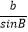 ,
, 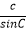 之间的关系,并证明.
之间的关系,并证明.
(2)猜想cosC与a,b,c之间的关系?并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,A(0,4),B(8,0),C(8,4).
⑴ 试说明四边形AOBC是矩形.
⑵ 在x轴上取一点D,将△DCB绕点C逆时针旋转90°得到
 (点
(点 与点D对应).
与点D对应).① 若OD=3,求点
 的坐标.
的坐标.② 连接AD'、OD',则AD'+OD'是否存在最小值,若存在,请直接写出最小值及此时点D'的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽暑假期间参加社会实践活动,从某批发市场以批发价每个
 元的价格购进
元的价格购进 个手机充电宝,然后每个加价
个手机充电宝,然后每个加价 元到市场出售.
元到市场出售. 求售出
求售出 个手机充电宝的总售价为多少元(结果用含
个手机充电宝的总售价为多少元(结果用含 ,
, 的式子表示)?
的式子表示)? 由于开学临近,小丽在成功售出
由于开学临近,小丽在成功售出 个充电宝后,决定将剩余充电宝按售价
个充电宝后,决定将剩余充电宝按售价 折出售,并很快全部售完.
折出售,并很快全部售完.①相比不采取降价销售,她将比实际销售多盈利多少元(结果用含
 、
、 的式子表示)?
的式子表示)?②若
 ,小丽实际销售完这批充电宝的利润率为________(利润率
,小丽实际销售完这批充电宝的利润率为________(利润率 利润
利润 进价
进价 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列给出四个命题:
①直角三角形的两边是方程y2-7y+12=0的两根,则它的第三边是5;
②若一元二次方程ax2+bx+c=0(a≠0)的系数a,c异号,则该方程有两个不相等的实数根;
③若一元二次方程(m-2)x2+x+m2-4=0有一个根为0,那么m=±2;
④已知一元二次方程ax2+bx+c=0(a≠0)中a,b,c满足a-b+c=0,4a+2b+c=0则方程的两根为x1=-1,x2=2;其中真命题的是__________(填序号)
相关试题

