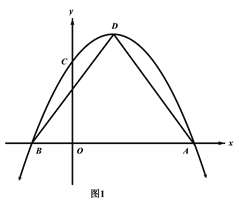
【题目】如图1,抛物线![]() 与x轴相交于A,B两点(点A在点B的右侧),与y轴交于点C,点D是抛物线的顶点,连接AD、BD.
与x轴相交于A,B两点(点A在点B的右侧),与y轴交于点C,点D是抛物线的顶点,连接AD、BD.
![]() 求△ABD的面积;
求△ABD的面积;
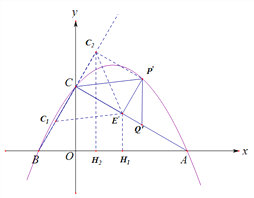
![]() 如图2,连接AC、BC,若点P是直线AC上方抛物线上一动点,过P作PE//BC交AC于点E,作PQ//y轴交AC于点Q,当△PQE周长最大时,将△PQE沿着直线AC平移,记移动中的△PQE为
如图2,连接AC、BC,若点P是直线AC上方抛物线上一动点,过P作PE//BC交AC于点E,作PQ//y轴交AC于点Q,当△PQE周长最大时,将△PQE沿着直线AC平移,记移动中的△PQE为![]() ,连接
,连接![]() ,求△PQE的周长的最大值及
,求△PQE的周长的最大值及![]() 的最小值;
的最小值;
![]() 如图3,点G为x轴正半轴上一点,且OG=OC,连接CG,过G作GH⊥AC于点H,将△CGH绕点O顺时针旋转
如图3,点G为x轴正半轴上一点,且OG=OC,连接CG,过G作GH⊥AC于点H,将△CGH绕点O顺时针旋转![]() (
(![]() ),记旋转中的△CGH为
),记旋转中的△CGH为![]() ,在旋转过程中,直线
,在旋转过程中,直线![]() ,
,![]() 分别与直线AC交于点M,N,
分别与直线AC交于点M,N, ![]() 能否成为等腰三角形?若能直接写出所有满足条件的
能否成为等腰三角形?若能直接写出所有满足条件的![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.


参考答案:
【答案】(1)A(6,0),B(-2,0),![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
, ![]() ,
, ![]() .
.
【解析】分析: ![]() 令
令![]() 即可求出点
即可求出点![]() 的坐标,求出顶点坐标,即可计算面积.
的坐标,求出顶点坐标,即可计算面积.
![]() 用待定系数法求出直线
用待定系数法求出直线![]() 的解析式,设点
的解析式,设点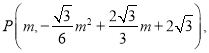 则
则
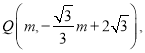 表示出
表示出![]() ,
, ![]() ,此时
,此时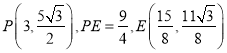 ,即可求出周长的最大值.
,即可求出周长的最大值.
如图, ![]() 平移后为
平移后为![]() ,再关于AC对称后为
,再关于AC对称后为![]() ,则
,则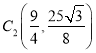 ,
,
求![]() 得最小值即可.
得最小值即可.
![]() 分三种请进行讨论.
分三种请进行讨论.
详解:(1)令![]() 解得:
解得: ![]()
![]()
![]()
即点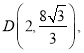
![]() .
.
(2)![]() ,
, ![]() ,
, ![]() ,
, 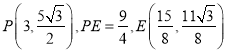
△PQE周长最大值为![]() ,
,
如图, ![]() 平移后为
平移后为![]() ,再关于AC对称后为
,再关于AC对称后为![]() ,则
,则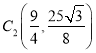 ,
,
![]()
![]()
(3)![]() ,
, ![]() ,
, ![]()
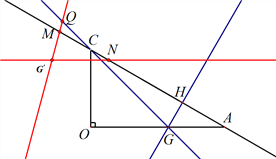
如图1,此时![]() ,
,![]() ,旋转角为
,旋转角为![]()

图1
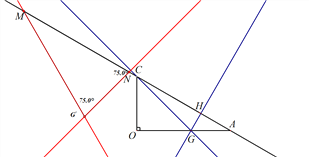
如图2,此时旋转角为![]() 的补角,
的补角, ![]() ,
,![]() ,故旋转角为120°
,故旋转角为120°
如图3,旋转角![]() 180-(30-15)=165°
180-(30-15)=165°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,正方形ABCD的面积等于100,l2与l3的距离为( )

A. 8B. 10C. 9D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,O为正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
(1)求证:△BCE≌△DCF;
(2)OG与BF有什么数量关系?证明你的结论;
(3)若GE·GB=4-2
 ,求正方形ABCD的面积.
,求正方形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=
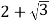 .
.其中正确的序号是 (把你认为正确的都填上).
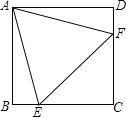
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要在平行四边形
 内作一个菱形.甲,乙两位同学的作法分别如下:
内作一个菱形.甲,乙两位同学的作法分别如下:
对于甲乙两人的作法,可判断( )
A.甲正确,乙错误B.甲错误,乙正确C.甲,乙均正确D.甲、乙均错误
相关试题

