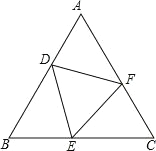
【题目】如图,△ABC 中,AB=AC,D、E、F 分别为 AB、BC、AC 上的点,且BD=CE,∠DEF=∠B.
(1)求证:∠BDE=∠CEF;
(2)当∠A=60°时,求证:△DEF 为等边三角形.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用外角的性质可得∠B+∠BDE=∠DEF+∠CEF,结合条件可证得结论;
(2)由条件可知∠B=∠C=60°,结合条件可证明△BDE≌△CEF,可证得DE=EF,则可证明△DEF为等边三角形.
(1)∵∠DEC是△BDE的一个外角,
∴∠B+∠BDE=∠DEF+∠CEF,
∵∠DEF=∠B,
∴∠BDE=∠CEF;
(2)由(1)可知∠BDE=∠CEF,
∵AB=AC,∠A=60°
∴∠B=∠C=60°,
∴∠DEF=60°,
在△BDE和△CEF中
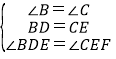 ,
,
∴△BDE≌△CEF(ASA),
∴DE=EF,
∴△DEF为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为方便市民出行,减轻城市中心交通压力,某市正在修建贯穿全城南北、东西的地铁1,2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元,且1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线、2号线每千米的平均造价分别是多少亿元;
(2)除1,2号线外,该市规划到2019年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到
 的位置,
的位置, ,
, ,平移距离为6,则阴影部分面积为
,平移距离为6,则阴影部分面积为


A. 24 B. 40 C. 42 D. 48
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,已知 AB=AC,BD 平分∠ABC,AE 为 BC 边的中线,AE、BD 相交于点 D,其中∠ADB=125°,求∠BAC 的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.

(1)求证:BC平分∠PBD;
(2)求证:BC2=ABBD;
(3)若PA=6,PC=6 ,求BD的长.
,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图形L.
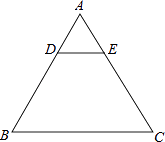
(1)求△ABC的面积;
(2)设AD=x,图形L的面积为y,求y关于x的函数解析式;
(3)已知图形L的顶点均在⊙O上,当图形L的面积最大时,求⊙O的面积.
相关试题

