【题目】如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
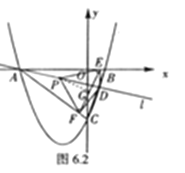
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.

参考答案:
【答案】(1)二次函数的解析式为:y=![]() x2+
x2+![]() x﹣6;
x﹣6;
(2)①P的运动路程为![]() ;②∠EPF的大小不会改变,理由见解析;
;②∠EPF的大小不会改变,理由见解析;
(3)C△PEF最小值为![]() .
.
【解析】试题分析:(1)由![]() 与
与![]() 轴分别交于A、B两点,且一元二次方程
轴分别交于A、B两点,且一元二次方程![]() 的两根为-8、2,可得点A、点B的坐标,即可得到OB的长,又由tan∠ABC=3,得到点C(0,-6),将 A、B、C的坐标代入二次函数中,即可得到二次函数解析式;
的两根为-8、2,可得点A、点B的坐标,即可得到OB的长,又由tan∠ABC=3,得到点C(0,-6),将 A、B、C的坐标代入二次函数中,即可得到二次函数解析式;
(2)①如图6.1,当l在AB位置时,P即为AB的中点H,当l运动到AC位置时,P即为AC的中点K,故P的运动路程为△ABC的中位线HK,在Rt△BOC中,由勾股定理得到BC的长,再由三角形中位线定理可得到HK的长,即P的运动路程;
②∠EPF的大小不会改变.由于,P为Rt△AED斜边AD的中点,故PE=![]() AD=PA,从而∠PAE=∠PEA=
AD=PA,从而∠PAE=∠PEA=![]() ∠EPD,同理有∠PAF=∠PFA=
∠EPD,同理有∠PAF=∠PFA=![]() ∠DPF,即可得到∠EPF=2∠EAF,故∠EPF的大小不会改变;
∠DPF,即可得到∠EPF=2∠EAF,故∠EPF的大小不会改变;
(3)设△PEF的周长为C,则![]() =PE+PF+EF=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,得到∠EPG=
=PE+PF+EF=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,得到∠EPG=![]() ∠EPF=∠BAC,由于tan∠BAC=
∠EPF=∠BAC,由于tan∠BAC=![]() ,故tan∠EPG=
,故tan∠EPG=![]() ,得到EG=
,得到EG=![]() PE,EF=
PE,EF=![]() PE=
PE=![]() AD,从而有
AD,从而有![]() =AD+EF=
=AD+EF=![]() AD=
AD=![]() AD,又当AD⊥BC时,AD最小,此时
AD,又当AD⊥BC时,AD最小,此时![]() 最小,由
最小,由![]() =30,得到AD=
=30,得到AD=![]() ,从而得到
,从而得到![]() 最小值.
最小值.
试题解析:(1)∵函数![]() 的图象与
的图象与![]() 轴分别交于A、B两点,且一元二次方程
轴分别交于A、B两点,且一元二次方程![]() 的两根为-8、2,∴A(-8,0)、B(2,0),即OB=2,又∵tan∠ABC=3,∴OC=6,即C(0,-6),将 A(-8,0)、B(2,0)代入
的两根为-8、2,∴A(-8,0)、B(2,0),即OB=2,又∵tan∠ABC=3,∴OC=6,即C(0,-6),将 A(-8,0)、B(2,0)代入![]() 中,解得:
中,解得: ![]() ,
, ![]() ,∴二次函数解析式为:
,∴二次函数解析式为: ![]() ;
;
(2)①如图6.1,当l在AB位置时,P即为AB的中点H,当l运动到AC位置时,P即为AC的中点K,∴P的运动路程为△ABC的中位线HK,∴HK=![]() BC,在Rt△BOC中,OB=2,OC=6,∴BC=
BC,在Rt△BOC中,OB=2,OC=6,∴BC=![]() ,∴HK=
,∴HK=![]() ,即P的运动路程为
,即P的运动路程为![]() ;
;
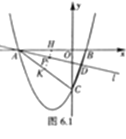
②∠EPF的大小不会改变.理由如下:
∵DE⊥AB,∴在Rt△AED中,P为斜边AD的中点,∴PE=![]() AD=PA,∴∠PAE=∠PEA=
AD=PA,∴∠PAE=∠PEA=![]() ∠EPD,同理可得:∠PAF=∠PFA=
∠EPD,同理可得:∠PAF=∠PFA=![]() ∠DPF,∴∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即∠EPF=2∠EAF,又∵∠EAF大小不变,∴∠EPF的大小不会改变;
∠DPF,∴∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即∠EPF=2∠EAF,又∵∠EAF大小不变,∴∠EPF的大小不会改变;
(3)设△PEF的周长为C,则![]() =PE+PF+EF,∵PE=
=PE+PF+EF,∵PE=![]() AD,PF=
AD,PF=![]() AD,∴
AD,∴![]() =AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,∴∠EPG=
=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,∴∠EPG=![]() ∠EPF=∠BAC,∵tan∠BAC=
∠EPF=∠BAC,∵tan∠BAC=![]() ,∴tan∠EPG=
,∴tan∠EPG=![]() ,∴EG=
,∴EG=![]() PE,EF=
PE,EF=![]() PE=
PE=![]() AD,∴
AD,∴![]() =AD+EF=
=AD+EF=![]() AD=
AD=![]() AD,又当AD⊥BC时,AD最小,此时
AD,又当AD⊥BC时,AD最小,此时![]() 最小,∵
最小,∵![]() =30,∴
=30,∴![]() BC·AD=30,∴AD=
BC·AD=30,∴AD=![]() ,∴
,∴![]() 最小值为:
最小值为: ![]() AD=
AD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某种新能源汽车的性能,对这种汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)这次被抽检的新能源汽车共有 辆;
(2)将图1补充完整;在图2中,C等级所占的圆心角是 度;
(3)估计这种新能源汽车一次充电后行驶的平均里程数为多少千米?(精确到千米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把两个边长相等的等边△ABC和△ACD拼成菱形ABCD,点E、F分别是射线CB、DC上的动点(E、F与B、C、D不重合),且始终保持BE=CF,连结AE、AF、EF.
(1)求证:①△ABE≌△ACF;②△AEF是等边三角形;
(2)①当点E运动到什么位置时,EF⊥DC?
②若AB=4,当∠EAB=15°时,求△CEF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线l:y=x+1交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,…记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…,则S8等于( )

A.28B.213C.216D.218
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣4x+4沿y轴向下平移9个单位,所得新抛物线与x轴正半轴交于点B,与y轴交于点C,顶点为D.求:(1)点B、C、D坐标;(2)△BCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆GF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上,
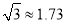 ,
, 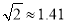 ,结果精确到0.1)
,结果精确到0.1)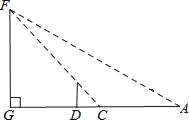
相关试题

