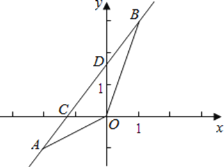
【题目】如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求该一次函数的解析式;
(2)求△AOB的面积.
参考答案:
【答案】(1) y=![]() x+
x+![]() ;(2)
;(2) ![]() .
.
【解析】
(1)求经过已知两点坐标的直线解析式,一般是按待定系数法步骤求得;(2)△AOB的面积=S△AOD+S△BOD,因为点D 是在y轴上,据其坐标特点可求出DO的长,又因为已知A、B点的坐标则可分别求三角形S△AOD与S△BOD的面积.
解:(1)把A(﹣2,﹣1),B(1,3)代入y=kx+b得![]() ,
,
解得![]() .所以一次函数解析式为y=
.所以一次函数解析式为y=![]() x+
x+![]() ;
;
(2)把x=0代入y=![]() x+
x+![]() 得y=
得y=![]() ,
,
所以D点坐标为(0,![]() ),
),
所以△AOB的面积=S△AOD+S△BOD=![]() ×y=
×y=![]() x+
x+![]() ;
;
×2+![]() ×y=
×y=![]() x+
x+![]() ×1=
×1=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图a是长方形纸带,∠DEF=24°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图 c中的∠CFE的度数是( )

A.104°B.106°C.108°D.110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,点M在x轴上,以点M为圆心,2.5长为半径的圆交y轴于A、B两点,交x轴于C(x1,0)、D(x2,0)两点,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的两根.
(1)求点C、D及点M的坐标;
(2)若直线y=kx+b切⊙M于点A,交x轴于P,求PA的长;
(3)⊙M上是否存在这样的点Q,使点Q、A、C三点构成的三角形与△AOC相似?若存在,请求出点的坐标,并求出过A、C、Q三点的抛物线的解析式;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
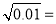 ____;(2)
____;(2)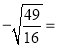 ____;(3)
____;(3)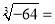 ____;(4)
____;(4)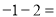 ____;(5)
____;(5)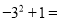 ____;(6)
____;(6)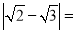 ____;(7)
____;(7)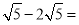 ____;(8)
____;(8)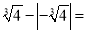 ____.
____. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个二元一次方程ax+by=c(a,b,c,为常数,且A,B均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标极点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,既二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,即2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).
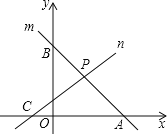
(1)如图,3x+3y=12,的图象为直线m,其与x轴交点A的坐标为____,其与y轴交点B的坐标为___;
(2)如图,ax+by=-5的图象为直线n,其与x轴交于C(-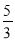 ,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值.
,0),与(1)中直线m交于P,若P的横坐标为1,求a和b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义运算a
 b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:①2
 (-2)=6 ②a
(-2)=6 ②a b=b
b=b a
a③若a+b=0,则(a
 a)+(b
a)+(b b)=2ab ④若a
b)=2ab ④若a b=0,则a=0.
b=0,则a=0.其中正确结论的序号是 (填上你认为所有正确结论的序号).
-
科目: 来源: 题型:
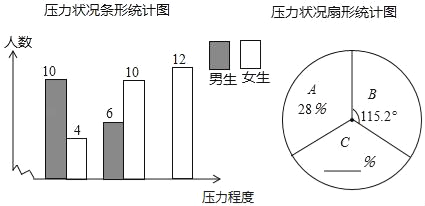
查看答案和解析>>【题目】中考科目已经发生变革,继中考增加体育实验之后,从2019年开始河南中考开始增设生物和地理科目,针对于此学校教务处王老师负责调查学生对此变革是否有压力,设置问题答案如下(A:大,B:一般,C:无),再将调查结果制成两幅不完统计图(如图所示),请根据统计图解答下列问题:
(1)本次调查中,王老师一共调查了 名学生;
(2)将条形统计图和扇形统计图补充完整;
(3)为了缓解学生压力,王老师从被调查的A类和B类学生中分别选取一名学生进行详细心理调查,请用合适的方法恰好选中一名男生和一名学生的概率.
相关试题

