【题目】如图,△ABC中,AB=AC,作以AB为直径的⊙O与边BC交于点D,过点D作⊙O的切线,分别交AC、AB的延长线于点E、F.
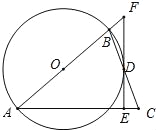
(1)求证:EF⊥AC;
(2)若BF=2,CE=1.2,求⊙O的半径.
参考答案:
【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)连接OD,AD,由切线的性质可得OD⊥EF,再利用圆周角定理证明AD⊥BC,根据等腰三角形的性质可证明OD∥AC,由平行线的性质即可得到EF⊥AC;
(2)设⊙O的半径为x,由O∥AC,可得:△ODF∽△AEF,根据相似三角形的性质:对应边的比值相等即可得到关于x的比例式,求出x的值即可.
试题解析:(1)连接OD,AD,
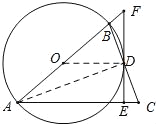
∵EF是⊙O的切线,
∴OD⊥EF.
又∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC.
又∵AB=AC,
∴BD=DC.
∴OD∥AC.
∴AC⊥EF.
(2)设⊙O的半径为x.
∵OD∥AE,
∴△ODF∽△AEF.
∴![]() ,即
,即![]() .
.
解得:x=3.
∴⊙O的半径为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. x3+x3=2x6 B. x6÷x2=x3 C. (﹣3x3)2=2x6 D. x2x﹣3=x﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,不能判定四边形是平行四边形的是( )
A. 对角线互相平分B. 两组对边分别相等
C. 对角线互相垂直D. 一组对边平行,一组对角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)已知二次函数y=x2-2x-3.
(1)用配方法将表达式化为y=(x-h)2+k的形式;
(2)求这个函数图象与x轴的交点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为__.(用含n的代数式表示,n为正整数)
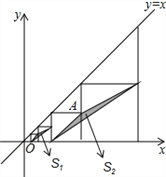
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.(2x)2=2x2
B.x2x3=x6
C.x5÷x3=x2
D.(x﹣2)3=x﹣5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为( )
A.﹣1
B.1
C.﹣3
D.3
相关试题

