Question

【题目】已知四边形ABCD，AD∥BC，AB⊥BC，AD=1，AB=2，BC=3．

（1）如图1，若P为AB边上一点以PD，PC为边作平行四边形PCQD，请问对角线PQ的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．

（2）若P为AB边上任意一点，延长PD到E，使DE=PD，再以PE，PC为边作平行四边形PCQE，请问对角线PQ的长是否也存在最小值？如果存在，请直接写出最小值，如果不存在，请说明理由．

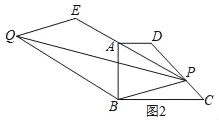
（3）如图2，若P为直线DC上任意一点，延长PA到E，使AE=AP，以PE、PB为边作平行四边形PBQE，请问对角线PQ的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．

Answer 1

【答案】（1）存在，理由见解析，当PQ⊥AB时，PQ的长最小，即为4．

（2）存在，理由见解析， 当PQ⊥AB时，PQ的长最小，即为5．

（3）存在，理由见解析，最小值为

【解析】试题分析：（1）在平行四边形PCQD中，设对角线PQ与DC相交于点G，则G是DC的中点，过点Q作QH⊥BC，交BC的延长线于H，使得Rt△ADP≌Rt△HCQ，进而求出最小值；

（2）设PQ与DC相交于点G，作QH⊥BC，交BC的延长线于H，可得Rt△ADP∽Rt△HCQ，进而求出最小值；

（3）设PQ与AB相交于点G，由平行线分线段成比例定理可得.作QH∥PD，交CB的延长线于H，过点C作CK⊥CD，交QH的延长线于K，可证△ADP∽△BHQ，

从而.过点D作DM⊥BC于M，则四边形ABND是矩形，可求∠DCM=45°，从而求出CD、CK的值，可知当D与P重合时的PQ长就是PQ的最小值.

解：（1）存在，理由如下：

如图2，在平行四边形PCQD中，设对角线PQ与DC相交于点G，

则G是DC的中点，

过点Q作QH⊥BC，交BC的延长线于H，

∵AD∥BC，AB⊥BC，

∴AD⊥AB，∠ADC=∠DCH，

即∠ADP+∠PDG=∠DCQ+∠QCH，

∵PD∥CQ，

∴∠PDC=∠DCQ，

∴∠ADP=∠QCH，

在△ADP和△HCQ中，，

∴△ADP≌△HCQ（AAS），

∴AD=HC，

∵AD=1，BC=3，

∴BH=4，

∴当PQ⊥AB时，PQ的长最小，即为4．

（2）存在，理由如下：

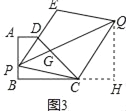
如图3，设PQ与DC相交于点G，

∵四边形PCQE是平行四边形，

∴PE∥CQ，PE=CQ，

∴，

∵PD=DE，

∴CQ=2PD，

∴=,

∴G是DC上一定点，

作QH⊥BC，交BC的延长线于H，

同（2）得：∠ADP=∠QCH，

∴Rt△ADP∽Rt△HCQ，

∴=，

∴CH=2，

∴BH=BC+CH=3+2=5，

∴当PQ⊥AB时，PQ的长最小，即为5．

（3）存在，理由如下：

如图4，设PQ与AB相交于点G，

∵四边形PBQE是平行四边形，

∴PE∥BQ，PE=BQ，

∴，

∵AE=PA，

∴BQ=2PA，

∴=

作QH∥PD，交CB的延长线于H，过点C作CK⊥CD，交QH的延长线于K，

∵AD∥BC，AB⊥BC，

∴∠ADP=∠QHC，∠DAP+∠PAG=∠QBH+∠QBG=90°，∠PAG=∠QBG，

∴∠QBH=∠PAD，

∴△ADP∽△BHQ，

∴=，

∵AD=1，

∴BH=2，

∴CH=BH+BC=2+3=5，

过点D作DM⊥BC于M，

则四边形ABND是矩形，

∴BM=AD=1，DM=AB=2

∴CM=BC﹣BM=3﹣1=2=DM，

∴∠DCM=45°，

∴∠KCH=45°，

∴CK=CHcos45°=5×=，

在Rt△CDM中，CD=2，

∴CK＞CD，

∴当PQ⊥CD时，PQ的长最小，但是，P点已经不在CD上了，到延长线上了，

∴当D与P重合时的PQ长就是PQ的最小值，

此时Q与H重合，PQ=HD===

∴最小值为