Question

【题目】如图，在等边△ABC内有一点D，AD=4，BD=3，CD=5，将△ABD绕A点逆时针旋转，使AB与AC重合，点D旋转至点E，则四边形ADCE的面积为（ 　 ）

A.12B.C.D.

Answer 1

【答案】C

【解析】

此题连接DE，先利用旋转和等边三角形的性质证明△ADE是等边三角形，根据题意，由△ADE是等边三角形依据勾股定理判定△CDE是直角三角形即可求四边形的面积．

如图：

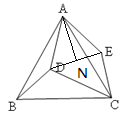
连接DE，过点A作AN 垂直DE于点E，

根据题意由旋转知AD=AE，∠BAD=∠CAE，

又∵等边△ABC中，∠BAC=60°，

∴∠BAD+∠CAD=∠CAE+∠CAD，

即∠BAC=∠DAE=60°，

∴△ADE是等边三角形，

∴DE=AD=4，

又BD=3，CD=5，

∴ ，

∴△CDE是直角三角形，

∵AD=4，∠ADE=60°，

∴∠DAN=30°，

∴DN=2，

由勾股定理得AN= ，

∵=，

，

，

∴，

即四边形ADCE的面积是，

故答案为：C．