Question

【题目】（本小题满分9分）

已知：△ABC是任意三角形．

（1）如图1所示，点M、P、N分别是边AB、BC、CA的中点．求证：∠MPN=∠A．

（2）如图2所示，点M、N分别在边AB、AC上，且， ，点P1、P2是边BC的三等分点，你认为∠MP1N+∠MP2N=∠A是否正确？请说明你的理由．

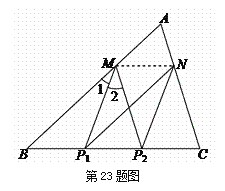
（3）如图3所示，点M、N分别在边AB、AC上，且， ，点P1、P2、……、P2009是边BC的2010等分点，则∠MP1N+∠MP2N+……+∠MP2009N=____________．

（请直接将该小问的答案写在横线上．）

Answer 1

【答案】（1）证明见解析；（2）正确；（3）∠A．

【解析】⑴证明：∵点M、P、N分别是AB、BC、CA的中点，

∴线段MP、PN是△ABC的中位线，

∴MP∥AN，PN∥AM， 1分

∴四边形AMPN是平行四边形， 2分

∴∠MPN=∠A. 3分

⑵∠MP1N+∠MP2N=∠A正确. 4分

如图所示，连接MN， 5分

∵，∠A=∠A，

∴△AMN∽△ABC，

∴∠AMN=∠B， ，

∴MN∥BC，MN=BC， 6分

∵点P1、P2是边BC的三等分点，

∴MN与BP1平行且相等，MN与P1P2平行且相等，MN与P2C平行且相等，

∴四边形MBP1N、MP1P2N、MP2CN都是平行四边形，

∴MB∥NP1，MP1∥NP2，MP2∥AC，

7分

∴∠MP1N=∠1，∠MP2N=∠2，∠BMP2=∠A，

∴∠MP1N+∠MP2N=∠1+∠2=∠BMP2=∠A.

8分

⑶∠A. 9分