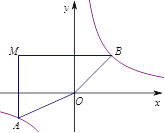
【题目】如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=![]() 的图象交于A、B两点,则四边形MAOB的面积为________.
的图象交于A、B两点,则四边形MAOB的面积为________.
参考答案:
【答案】10
【解析】试题分析:设点A的坐标为(a,b),点B的坐标为(c,d),根据反比例函数y=![]() 的图象过A,B两点,所以ab=4,cd=4,进而得到S△AOC=
的图象过A,B两点,所以ab=4,cd=4,进而得到S△AOC=![]() |ab|=2,S△BOD=
|ab|=2,S△BOD=![]() |cd|=2,
|cd|=2,
S矩形MCDO=3×2=6,根据四边形MAOB的面积=S△AOC+S△BOD+S矩形MCDO,即可解答.
解:如图,
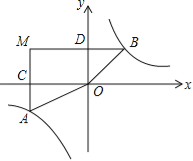
设点A的坐标为(a,b),点B的坐标为(c,d),
∵反比例函数y=![]() 的图象过A,B两点,
的图象过A,B两点,
∴ab=4,cd=4,
∴S△AOC=![]() |ab|=2,S△BOD=
|ab|=2,S△BOD=![]() |cd|=2,
|cd|=2,
∵点M(﹣3,2),
∴S矩形MCDO=3×2=6,
∴四边形MAOB的面积=S△AOC+S△BOD+S矩形MCDO=2+2+6=10,
故答案为:10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A. x6x2=x12B. x2+x2=2x2
C. (﹣c)8÷(﹣c)6=﹣c2D. (ab3)2=ab6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式从左到右的变形是因式分解的是( )
A. x(x﹣2)=x2﹣2xB. x2+2xy+1=x(x+2y)+1
C. 15a2b=3a25bD. a2b2﹣1=(ab+1)(ab﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为有效开展阳光体育活动,云洱中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.已知九年级一班在8场比赛中得到13分,问九年级一班胜、负场数分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
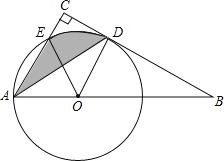
(1)求证:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 相等的角是直角
B. 若a⊥b,a⊥c,则b⊥c
C. 两直线平行,同位角互补
D. 互补的两个角不能都是锐角
相关试题

