【题目】(满分14分)已知,四边形ABCD是正方形,点F是边AB、BC上一动点,DE⊥DF,且DE=DF,M为EF的中点.
当点F在边AB上时(如图).
求证:点E在BC直线上;
若AD=a,AF=b,并满足![]() .
.
求a,b的值及MC的长;
当点F在BC上时(如图),求![]() 的值.
的值.


(图) (图)
参考答案:
【答案】(1)①见解析,②![]() ;(2)
;(2)![]()
【解析】试题分析:(1)①连接CE,证明△ADF≌△CDE,得到∠DCE=∠DAF=90°即可;②作FK∥MC,证明CM=![]() FK,求出FK=
FK,求出FK=![]() BF即可;(2)过点E作CD的平行线分别交AD、BC的延长线于K、Q,EN∥MC,根据平行线等分线段定理即可解答.
BF即可;(2)过点E作CD的平行线分别交AD、BC的延长线于K、Q,EN∥MC,根据平行线等分线段定理即可解答.
试题解析:
(1)①如图①,连接CE,

∵∠ADC=90°,DE⊥DF,
∴∠ADF=∠CDE,
在△ADF和△CDE中,
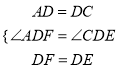 ,
,
∴△ADF≌△CDE,
∴∠DCE=∠DAF=90°,
∴点E在直线BC上;
②如图①,作FK∥MC,∵M为EF的中点,
∴CM=![]() FK,
FK,
∵∠DMB=∠DCB=90°,
∴D、M、C.B四点共圆,
∴∠MCD=∠MBD=45°,
∴∠BKF=45°,
∵BF=2,∴FK=![]() ,
,
∴CM=![]() FK=
FK=![]() ;
;
(2)过点E作CD的平行线分别交AD、BC的延长线于K、G,EN∥MC,
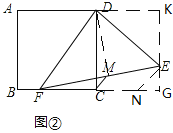
∵M为EF的中点,
∴CM=![]() NE,FC=CN,
NE,FC=CN,
∴NG=EG=BF,
![]() =
=![]() =
=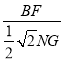 =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学胜在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整).

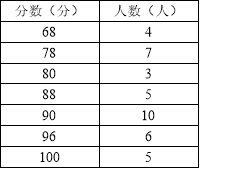
(1)补全条形统计图;
(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;
(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?
(4)小明的成绩为88分,他的成绩如何,为什么?
-
科目: 来源: 题型:
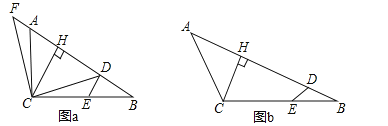
查看答案和解析>>【题目】如图,在△ABC中,BC>AC,点E在BC上,CE=CA,点D在AB上,连接DE,∠ACB+∠ADE=180°,作CH⊥AB,垂足为H.
(1)如图a,当∠ACB=90°时,连接CD,过点C作CF⊥CD交BA的延长线于点F.
①求证:FA=DE;
②请猜想三条线段DE,AD,CH之间的数量关系,直接写出结论;
(2)如图b,当∠ACB=120°时,三条线段DE,AD,CH之间存在怎样的数量关系?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市一月份营业额为100万元,一月、二月、三月的营业额共500万元,如果平均每月增长率为x,则由题意可列方程( )
A. 100(1+x)2=500
B. 100+1002x=500
C. 100+1003x=500
D. 100[1+(1+x)+(1+x)2]=500
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,全球每分钟约有8500000吨污水排入江河湖海,将8500000用科学记数法表示为吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)观察一列数a1=3,a2=32,a3=33,a4=34,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是_______;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a6=_______,an=_______;(可用幂的形式表示)
(2)如果想要求l+2+22+23+...+210的值,可令S10=l+2+22+23+...+210①,将①式两边同乘以2,得_______②,由②减去①式,得S10=_______.
(3)若(1)中数列共有20项,设S20=3+32+33+34+…+320,请利用上述规律和方法计算S20的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD//BC,E是BC的中点,AD=5,BC=12,CD=
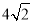 ,∠C=45°,点P是BC边上一动点,设PB的长为x。
,∠C=45°,点P是BC边上一动点,设PB的长为x。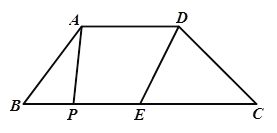
(1)梯形ABCD的面积为_________;
(2)当x的值为___________时,以点P、A、D、E为顶点的四边形为直角梯形;
(3)当x的值为___________时,以点P、A、D、E为顶点的四边形为平行四边形;
(4)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由。
相关试题

