【题目】如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E. 
(1)求证:MD=ME;
(2)填空:连接OE,OD,当∠A的度数为时,四边形ODME是菱形.
参考答案:
【答案】
(1)证明:在Rt△ABC中,点M是AC的中点,
∴MA=MB,
∴∠A=∠MBA;
∵四边形ABED是圆内接四边形,
∴∠ADE+∠ABE=180°,
而∠ADE+∠MDE=180°,
∴∠MDE=∠MBA;
同理可得∠MED=∠A,
∴∠MDE=∠MED,
∴MD=ME
(2)60°
【解析】解:(2)当∠A=60°时,
则∠ABM=60°,
∴△OAD和△OBE为等边三角形,
∴∠BOE=60°,
∴∠BOE=∠A,
∴OE∥AC,
同理可得OD∥BM,
∴四边形DOEM为平行四边形,
而OD=OE,
∴四边形ODME是菱形.
故答案为60°.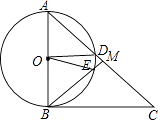
(1)利用直角三角形斜边上的中线性质得MA=MB,则∠A=∠MBA,再利用圆内接四边形的性质证明∠MDE=∠MED,于是得到MD=ME;(2)先证明△OAD和△OBE为等边三角形,再证明四边形DOEM为平行四边形,然后加上OD=OE可判断四边形ODME是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:x
…
﹣3
-

﹣2
﹣1
0
1
2

3
…
y
…
3

m
﹣1
0
﹣1
0

3
…
其中m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出2条函数的性质;
(4)进一步探究函数图象发现:
①函数图象与x轴有个交点,所对应的方程x2﹣2|x|=0有个实数根;
②方程x2﹣2|x|=2有个实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;
(2)△ABC的面积是 .
(3)点P(a+1,b-1)与点C关于x轴对称,则a= ,b= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )
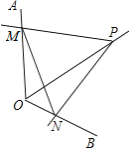
A. 4B. 3C. 2D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2 , 请直接写出旋转中心的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)2x2﹣8x=0.
(2)x2﹣3x﹣4=0.
求出抛物线的开口方向、对称轴、顶点坐标.
(3)y= x2﹣x+3(公式法).
x2﹣x+3(公式法). -
科目: 来源: 题型:
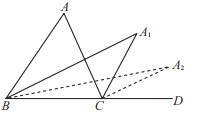
查看答案和解析>>【题目】如图,在
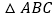 中,
中,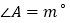 ,
,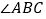 和
和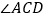 的平分线交于点
的平分线交于点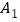 ,得
,得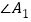 ;
;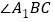 和
和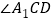 的平分线交于点
的平分线交于点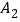 ,得
,得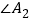 ;…;
;…;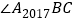 和
和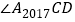 的平分线交于点
的平分线交于点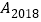 ,则
,则 =___________.
=___________.
相关试题

