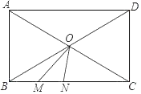
【题目】如图,O为矩形ABCD对角线AC,BD的交点,AB=9,AD=18,M,N是直线BC上的动点,且MN=3,则OM+ON最小值=___.
参考答案:
【答案】3![]() .
.
【解析】
通过作图得到平行四边形MNQP,由平行四边形MNQP的性质得到OM+ON=QN+ON,从而得到当O,N,Q在同一直线上时,OM+ON最小,即OM+ON=OQ;由轴对称的性质得到OP长度,最后根据勾股定理得到OQ的值,从而得到答案.
如图所示,作点O关于BC的对称点P,连接PM,将MP沿着MN的方向平移MN长的距离,得到NQ,连接PQ,

则四边形MNQP是平行四边形,
∴MN=PQ=3,PM=NQ=MO,
∴OM+ON=QN+ON,
当O,N,Q在同一直线上时,OM+ON的最小值等于OQ长,
连接PO,交BC于E,
由轴对称的性质,可得BC垂直平分OP,
又∵矩形ABCD中,OB=OC,
∴E是BC的中点,
∴OE是△ABC的中位线,
∴OE=![]() AB=4.5,
AB=4.5,
∴OP=2×4.5=9,
又∵PQ∥MN,
∴PQ⊥OP,
∴Rt△OPQ中,OQ=![]() =
=![]() =3
=3![]() ,
,
∴OM+ON的最小值是3![]() ,
,
故答案为:3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )
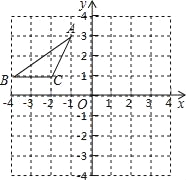
A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1) C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
-
科目: 来源: 题型:
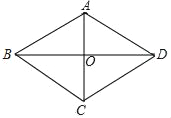
查看答案和解析>>【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠BAO=∠DAO.
(1)求证:平行四边形ABCD是菱形;
(2)请添加一个条件使菱形ABCD为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=
 S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,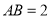 ,
,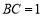 ,点
,点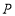 从点
从点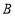 出发,沿
出发,沿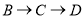 向终点
向终点 匀速运动,设点
匀速运动,设点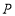 走过的路程为
走过的路程为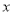 ,
,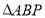 的面积为
的面积为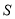 ,能正确反映
,能正确反映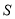 与
与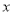 之间函数关系的图象是( )
之间函数关系的图象是( )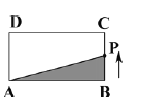
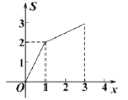
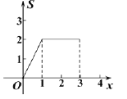
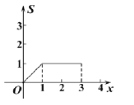
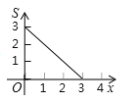
A. B. C. D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以正方形
 的顶点
的顶点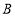 为直角顶点,作等腰直角三角形
为直角顶点,作等腰直角三角形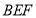 ,连接
,连接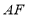 、
、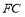 ,当
,当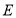 、
、 、
、 三点在--条直线上时,若
三点在--条直线上时,若 ,
,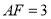 ,则正方形
,则正方形 的面积是( )
的面积是( )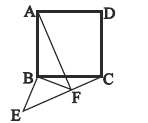
A.
 B.
B. C.
C. D.
D.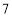
相关试题

