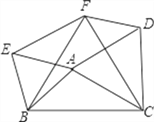
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF。
(1)求证:△EBF≌△DFC;
(2)求证:四边形AEFD是平行四边形;
(3)①△ABC满足_____________________时,四边形AEFD是菱形。(无需证明)
②△ABC满足_______________________时,四边形AEFD是矩形。(无需证明)
③△ABC满足_______________________时,四边形AEFD是正方形。(无需证明)
参考答案:
【答案】(1)证明见解析;
(2)证明见解析;
(3)①AB=AC②∠BAC=150°,③AB=AC,∠BAC=150°
【解析】试题分析:(1)由三角形BCF与三角形AEB为等边三角形,利用等边三角形的性质得到两对边相等,一对角相等,利用等式的性质得到夹角相等,利用SAS即可得证;
(2)可通过证△EFB≌△ACB,得EF=AC=AD;然后证△CDF≌△CAB,得DF=AB=AE;从而证得四边形ADFE的两组对边分别相等,即可得出ADFE是平行四边形;
(3)①当∠BAC=150°,由此可求得∠EAD的度数,则可得ADFE是矩形;
②当AE=AD时,ADFE是菱形;
③当ADFE是正方形时,∠EAD=90°,且AE=AD,联立(2)(3)的结论即可.
试题解析:(1)连接EF、DF,
∵△ABE、△CBF是等边三角形,
∴BE=AB,BF=CB,∠EBA=∠FBC=60°;
∴∠EBF=∠ABC=60°-∠ABF;
∴△EFB≌△ACB;
∴EF=AC=AD;
(2)同理由△CDF≌△CAB,得DF=AB=AE;
(3)①由AE=DF,AD=EF即可得出四边形AEFD是平行四边形;若∠BAC=150°,则平行四边形AEFD是矩形;
②由(2)知四边形AEFD是平行四边形,则∠EAD=90°时,可得平行四边形AEFD是矩形,∴∠BAC=360°-60°-60°-90°=150°,即△ABC满足∠BAC=150°时,四边形AEFD是矩形;
③综合①②的结论知:当△ABC是顶角∠BAC是150°的等腰三角形时,四边形AEFD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中错误的是( )
A. 两组对边分别相等的四边形是平行四边形 B. 对角线相等的平行四边形是矩形
C. 一组邻边相等的平行四边形是菱形 D. 对角线相等且互相垂直的四边形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2-9x+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为( )
A. 12 B. 12或15 C. 15 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. “买一张彩票中大奖”是随机事件
B. 不可能事件和必然事件都是确定事件
C. “穿十条马路连遇十次红灯”是不可能事件
D. “太阳东升西落”是必然事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】调查作业:了解你所住小区家庭5月份用气量情况.
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2-5之间,这300户家庭的平均人数均为3.4.
小天、小东、小芸各自对该小区家庭5月份用气量情况进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1 抽样调查小区4户家庭5月份用气量统计表 (单位:
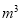 )
)
表2 抽样调查小区15户家庭5月份用气量统计表 (单位:
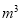 )
)
表3 抽样调查小区15户家庭5月份用气量统计表 (单位:
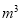 )
)
根据以上材料回答问题:
小天、小东和小芸三人中,哪一位同学抽样调查的数据能较好地反映出该小区家庭5月份用气量情况,并简要说明其他两位同学抽样调查地不足之处.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
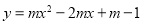 (m>0)与x轴的交点为A,B.
(m>0)与x轴的交点为A,B.(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
相关试题

