【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由。
参考答案:
【答案】
(1)
【解答】证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°.
∵∠BCD+∠DCE=180°,
∴∠BCD=∠DCE=90°.
又∵CG=CE,
∴△BCG≌△DCE.
(2)
【解答】四边形E′BGD是平行四边形.理由如下:
∵△DCE绕D顺时针旋转90°得到△DAE′,
∴CE=AE′.
∵CE=CG,
∴CG=AE′.
∵四边形ABCD是正方形,
∴BE′∥DG,AB=CD.
∴AB-AE′=CD-CG.
即BE′=DG.
∴四边形E′BGD是平行四边形.
【解析】(1)由正方形ABCD,得BC=CD,∠BCD=∠DCE=90°,又CG=CE,所以△BCG≌△DCE(SAS).(2)由(1)得BG=DE,又由旋转的性质知AE′=CE=CG,所以BE′=DG,从而证得
四边形E′BGD为平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于命题若a2=b2 , 则a=b,下面四组关于a,b的值中,能说明这个命题属于假命题的是( )
A. a=3,b=3
B. a=-3,b=-3
C. a=3,b=-3
D. a=-3,b=-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a2+ab=5,ab+b2=4,则a2+2ab+b2的值为 .
-
科目: 来源: 题型:
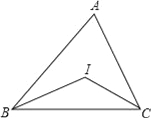
查看答案和解析>>【题目】如图,△ABC中,∠ABC、∠ACB的平分线相交于点I.
(1)若∠ABC=70°,∠ACB=50°,则∠BIC=__;
(2)若∠ABC+∠ACB=120°,则∠BIC=__;
(3)若∠A=60°,则∠BIC=__;
(4)若∠A=100°,则∠BIC=__;
(5)若∠A=n°,则∠BIC=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出的四个命题中,假命题是( )
A. 如果a=3,那么|a|=3
B. 如果x2=4,那么x=±2
C. 如果(a-1)(a+2)=0,那么a-1=0或a+2=0
D. 如果(a-1)2+(b+2)2=0,那么a=1或b=-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果|a+2|+(b﹣1)2=0,那么(a+b)2013的值是( )
A.﹣2013
B.2013
C.﹣1
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=
 .其中正确的结论有( )
.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
相关试题

