【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.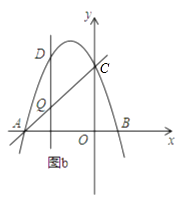
参考答案:
【答案】
(1)
解:把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得
![]() ,
,
解得 ![]() .
.
故该抛物线的解析式为:y=﹣x2﹣2x+3.
(2)
解:由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).
∵S△AOP=4S△BOC,
∴ ![]() ×3×|﹣x2﹣2x+3|=4×
×3×|﹣x2﹣2x+3|=4× ![]() ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x﹣7=0,
解得x=﹣1或x=﹣1±2 ![]() .
.
则符合条件的点P的坐标为:(﹣1,4)或(﹣1+2 ![]() ,﹣4)或(﹣1﹣2
,﹣4)或(﹣1﹣2 ![]() ,﹣4)
,﹣4)
(3)
解:设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,
得 ![]() ,
,
解得 ![]() .
.
即直线AC的解析式为y=x+3.
设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),
QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+ ![]() )2+
)2+ ![]() ,
,
∴当x=﹣ ![]() 时,QD有最大值
时,QD有最大值 ![]()
【解析】(1)把点A、C的坐标分别代入函数解析式,列出关于系数的方程组,通过解方程组求得系数的值;(2)设P点坐标为(x,﹣x2﹣2x+3),根据S△AOP=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;(3)先运用待定系数法求出直线AC的解析式为y=x+3,再设Q点坐标为(x,x+3),则D点坐标为(x,x2+2x﹣3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D.
(1)若△BCD的周长为8,求BC的长;
(2)若∠A=40°,求∠DBC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形
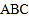 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: )
)例2 等腰三角形
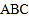 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: 或
或 或
或 )
)张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形
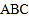 中,
中, ,求
,求 的度数.
的度数.(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,
 的度数不同,得到
的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形 中,设
中,设 ,当
,当 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索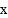 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC和△ECD都是等边三角形

(1)如图1,若B、C、D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中,将它绕点C顺时针旋转a角,旋转后的矩形记为矩形EDCF.在旋转过程中,
(1)如图①,当点E在射线CB上时,E点坐标为;
(2)当△CBD是等边三角形时,旋转角a的度数是(a为锐角时);
(3)如图②,设EF与BC交于点G,当EG=CG时,求点G的坐标;
(4)如图③,当旋转角a=90°时,请判断矩形EDCF的对称中心H是否在以C为顶点,且经过点A的抛物线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=______cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于
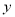 轴对称的
轴对称的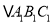 ,并写出
,并写出 三个顶点的坐标:
三个顶点的坐标: 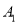 ( ),
( ),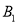 ( ),
( ),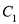 ( );
( );(2)直接写出△ABC的面积为 ;
(3)在
 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.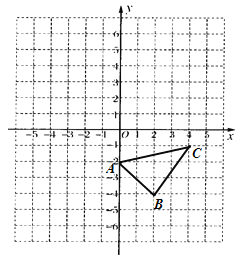
相关试题

