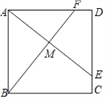
【题目】如图,正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M.求证:AE⊥BF.
参考答案:
【答案】证明见解析.
【解析】试题分析:首先证明△ABF≌△DAE(SAS),即可推出∠AFB=∠DEA,由∠D=90°,推出∠DEA+∠DAE=90°,推出∠AFB+∠DAE=90°,推出∠AMF=180°-90°=90°.
试题解析:证明:∵四边形ABCD是正方形,
∴∠BAD=∠ADE=90°,AD=AB=DC,
∵DF=CE,
∴AF=DE,
∵在△ABF和△DAE中,
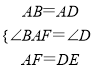 ,
,
∴△ABF≌△DAE(SAS);
∴∠AFB=∠DEA,
∵∠D=90°,
∴∠DEA+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AMF=180°﹣90°=90°,
∴AE⊥BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A. (﹣3,7) B. (﹣1,7) C. (﹣4,10) D. (0,10)
-
科目: 来源: 题型:
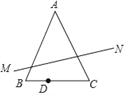
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=45°,BC=2,D是线段BC上的一个动点,点D是关于直线AB、AC的对称点分别为M、N,则线段MN长的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某课题小组为了了解某品牌电动自行车的销售情况,对某专卖店第一季度该品牌A、B、C、D四种型号的销售做了统计,绘制成如下两幅统计图(均不完整)
(1)该店第一季度售出这种品牌的电动自行车共多少辆?
(2)把两幅统计图补充完整;
(3)若该专卖店计划订购这四款型号的电动自行车1800辆,求C型电动自行车应订购多少辆?

-
科目: 来源: 题型:
查看答案和解析>>【题目】芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,
 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系的图象如图所示.
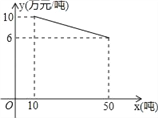
(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当生产这种产品每吨的成本为7万元时,求该产品的生产数量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高足球基本功,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)请用树状图列举出三次传球的所有可能情况;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
相关试题

