【题目】四边形ABCD的四个顶点分别作对角线AC、BD的平行线,所围成的四边形EFGH显然是平行四边形.
(1)当四边形ABCD分别是菱形、矩形、正方形时,相应的平行四边形EFGH一定是“菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:
四边形ABCD | 菱形 | 矩形 | 正方形 |
平行四边形EFGH |
(2)反之,当用上述方法所围成的平行四边形EFGH分别是矩形、菱形、正方形时,相应的原四边形ABCD必须满足怎样的条件?

解:(1)直接在上表中填写
(2)请在下表中填写
平行四边形EFGH | 矩形 | 菱形 | 正方形 |
四边形ABCD |
参考答案:
【答案】(1)
四边形ABCD | 菱形 | 矩形 | 正方形 |
平行四边形EFGH | 矩形 | 菱形 | 正方形 |
(2)
平行四边形EFGH | 矩形 | 菱形 | 正方形 |
四边形ABCD | BD⊥AC | AC=BD | BD⊥AC且 AC=BD |
【解析】
试题分析:可以根据对角线垂直且互相平分的是菱形,对角线相等且互相平分的是矩形,对角线相等,垂直且互相平分的是正方形.
试题解析:(1)四边形ABCD是菱形时,平行四边形EFGH是矩形;四边形ABCD是矩形时,平行四边形EFGH是菱形;四边形ABCD是正方形时,平行四边形EFGH是正方形;
(2)当平行四边形EFGH是菱形时,四边形ABCD应满足对角线相等;当平行四边形EFGH是矩形时,四边形ABCD应满足对角线垂直;当平行四边形EFGH是正方形时,四边形ABCD应满足对角线相等且互相垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
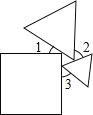
A.90° B.100° C.130° D.180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AC与BD交于点O,点E,F都在BD上,BE=DF.
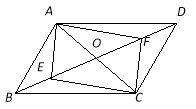
(1)求证:四边形AECF是平行四边形.
(2)若AB⊥AC,AB=4,AC=6,当□AECF是矩形时,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm.点P从点A出发,以3cm/s的速度沿折线ABCD方向运动,点Q从点D出发,以2cm/s的速度沿线段DC向点C运动.已知P,Q两点同时出发,当点Q到达点C时,P,Q停止运动,设运动时间为t(s).

(1)、求CD的长.
(2)、当四边形PBQD为平行四边形时,求四边形PBQD的周长.
(3)、当点P在折线BCD上运动时,是否存在某一时刻,使得△BPQ的面积为16cm2?若存在,请求出满足条件的t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.

(1)如图1,若AB∥ON,则①∠ABO的度数是 ;
②当∠BAD=∠ABD时,x= ;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生物学家发现一种病毒的长度约为0.00000403mm,数0.00000403用科学记数法表示为( )
A. 4.03×10﹣7 B. 4.03×10﹣6 C. 40.3×10﹣8 D. 430×10﹣9
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2﹣6x+m=0有两个相等的实数根,则实数m= .
相关试题

