Question

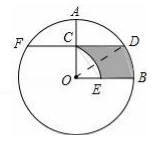
【题目】如图，在⊙O中，半径OA⊥OB，过点OA的中点C作FD∥OB交⊙O于D、F两点，且CD=，以O为圆心，OC为半径作，交OB于E点．

（1）求⊙O的半径OA的长；

（2）计算阴影部分的面积．

Answer 1

【答案】(1)2；（2）.

【解析】

试题分析：（1）首先证明OA⊥DF，由OD=2CO推出∠CDO=30°，设OC=x，则OD=2x，利用勾股定理即可解决问题．（2）根据S圆=S△CDO+S扇形OBD﹣S扇形OCE计算即可．

试题解析：（1）连接OD，

∵OA⊥OB，

∴∠AOB=90°，

∵CD∥OB，

∴∠OCD=90°，

在RT△OCD中，∵C是AO中点，CD=，

∴OD=2CO，设OC=x，

∴x2+（）2=（2x）2，

∴x=1，

∴OD=2，

∴⊙O的半径为2．

（2）∵sin∠CDO==，

∴∠CDO=30°，

∵FD∥OB，

∴∠DOB=∠ODC=30°，

∴S圆=S△CDO+S扇形OBD﹣S扇形OCE

=×+﹣

=+．