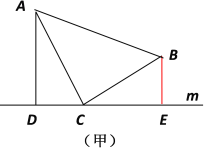
【题目】如图:△ABC中CA=CB, ∠ACB=90°,直线m经过点C,AD⊥m,BE⊥m,垂足分别是点D、E.
(1)在图(甲)中,求证:△ACD≌△CBE.你能探索出线段AD、BE、DE之间的关系吗?
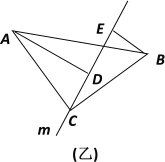
(2)在图(乙)中上面的结论还成立吗?为什么?
参考答案:
【答案】(1)证明见解析,DE=AD+BE;(2)成立,理由见解析
【解析】试题分析:(1)根据垂直的性质,可根据“AAS”证明△ADC ≌△CEB,然后根据全等三角形的性质证明即可;
(2)同(1)的证明方法直接可证明.
试题解析:DE=AD+BE
(1)证明:∵AD⊥m ∴∠DAC﹢∠ACD=∠ADC=90°
∵∠ACB=90°∴∠ACD+∠BCE=90°
∴∠DAC=∠BCE
∵BE⊥m ∴∠BEC=90°
在△ADC 和△CEB中
∠ADC=∠CEB=90°
∠DAC=∠BCE
CA=CB
∴△ADC ≌△CEB (AAS)
∴AD=CE DC=BE (全等三角形的对应边相等)
∵DE=DC+CE ∴DE=AD+BE
(2) 在(乙)图中上面的结论仍然成立.
证明:∵AD⊥m ∴∠ADC=90°∠ACD+∠CAD=90°
∵BE⊥m ∴∠CEB=90°
∵∠ACB=90°∴∠ACD+∠BCE=90°
∴∠DAC=∠ECB
在△ADC 和△CEB中
∠ADC=∠CEB=90°
∠DAC=∠ECB
CA=CB
∴△ADC ≌△CEB (AAS)
∴AD=CE DC=BE (全等三角形的对应边相等)
∵DE=DC+CE ∴DE=AD+BE
-
科目: 来源: 题型:
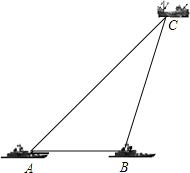
查看答案和解析>>【题目】如图,在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持10海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一不明国籍的渔船C,求此时渔船C与海监船B的距离是多少.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装原价为200元,连续两次涨价a%后,售价为242元,则a的值为( )
A. 10 B. 9 C. 5 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】将方程3x2+6x-1=0配方,变形正确的是( )
A. (3x+1)2-1=0 B. (3x+1)2-2=0 C. 3(x+1)2-4=0 D. 3(x+1)2-1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式﹣6ab+18abc+24ab2的一个因式是﹣6ab,则其余的因式是( )
A. 1﹣3c﹣4b B. ﹣1﹣3c+4b C. 1+3c﹣4b D. ﹣1﹣3c﹣4b
-
科目: 来源: 题型:
查看答案和解析>>【题目】点M (﹣5,3)关于x轴的对称点的坐标是( )
A.(﹣5,﹣3)
B.(5,﹣3)
C.(5,3)
D.(﹣5,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】若|3x+6|+(3﹣y)2=0,求多项式3y2﹣x2+(2x﹣y)﹣(x2+3y2)的值(先化简,再求值).
相关试题

