搜索
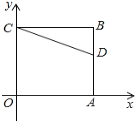
【题目】如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D(5,3)在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D’的坐标是( )
A.(2，10)B.(-2，0)C.(2，10)或(-2，0)D.(10，2)或(-5，2)
参考答案：
【答案】C
【解析】
根据题意，分顺时针旋转和逆时针旋转两种情况，求出点D′到x轴、y轴的距离，即可判断出旋转后点D的对应点D′的坐标是多少即可．
解：∵点D（5，3）在边AB上，
∴BC=5，BD=5-3=2，
①若顺时针旋转，则点D′在x轴上，OD′=2，
所以，D′（-2，0），
②若逆时针旋转，则点D′到x轴的距离为10，到y轴的距离为2，
所以，D′（2，10），
综上所述，点D′的坐标为（2，10）或（-2，0）．
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
（2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在对边不相等的四边形中，若四边形的两条对角线互相垂直，那么顺次连结四边形各边中点得到的四边形是( )
A.梯形B.矩形C.菱形D.正方形
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S△CEF=2S△ABE．其中正确结论有【 】个．
A．2 B．3 C．4 D．5
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=-x2+bx+c与x轴交于点A(-1.0)和点B(3,0) ,与y轴交于点C，连接BC交抛物线的对称轴于点E，D是抛物线的顶点.
(1)求此抛物线的解析式
(2)直接写出点C和点D的坐标
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△CDE，求P点坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在同一直角坐标系中，二次函数y=x2-2x-3的图象与两坐标轴分别交于点A点 B和点C，一次函数的图象与抛物线交于B、C两点.
（1）将这个二次函数化为
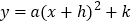的形式为 。（2）当自变量
满足 时，两函数的函数值都随增大而增大。（3）当自变量
满足 时，一次函数值大于二次函数值。（4）当自变量
满足 时，两个函数的函数值的积小于0。 -
科目： 来源： 题型：
查看答案和解析>>【题目】若一个函数的解析式等于另两个函数解析式的和，则这个函数称为另两个函数的“生成函数”。现有关于x的两个二次函数y1、y2，且y1＝a(x－m)2＋4(m>0)，y1、y2的“生成函数”为：y＝x2＋4x＋14；当x＝m时，y2＝15；二次函数y2的图象的顶点坐标为(2，k)。
(1)求m的值；
(2)求二次函数y1、y2的解析式。
相关试题
