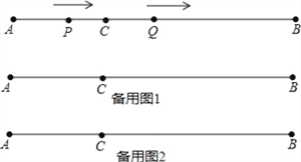
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

参考答案:
【答案】 4 8
【解析】试题分析:(1)由于AB=12cm,点C是线段AB上的一点,BC=2AC,则AC+BC=3AC=AB=12cm,依此即可求解;
(2)分别表示出AP、PQ,然后根据等量关系AP=PQ列出方程求解即可;
(3)分相遇前、相遇后以及到达B点返回后相距1cm四种情况列出方程求解即可.
试题解析:(1)∵AB=12cm,点C是线段AB上的一点,BC=2AC,
∴AC+BC=3AC=AB=12cm,
∴AC=4cm,BC=8cm;
(2)由题意可知:AP=3t,PQ=4﹣(3t﹣t),
则3t=4﹣(3t﹣t),
解得:t=![]() .
.
答:当t=![]() 时,AP=PQ.
时,AP=PQ.
(3)∵点P、Q相距的路程为1cm,
∴(4+t)﹣3t=1(相遇前)或3t﹣(4+t)=1(第一次相遇后),
解得t=![]() 或t=
或t=![]() ,
,
当到达B点时,第一次相遇后点P、Q相距的路程为1cm,
3t+4+t=12+12﹣1
解得:t=![]() .
.
答:当t为![]() ,
, ![]() ,
, ![]() 时,PQ=1cm.
时,PQ=1cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在矩形ABCD中,AB=8,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
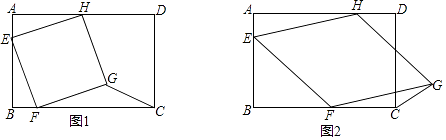
(1)如图1,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图2,当四边形EFGH为菱形时,设BF=x,△GFC的面积为S,求S关于x的函数关系式,并写出函数的定义域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则 t的值为 秒(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,试探索:在旋转过程中,∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请求出差的变化范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四川雅安发生地震后,某校学生会向全校1900名学生发起了“心系雅安”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列是问题:
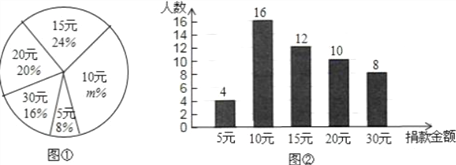
(1)本次接受随机抽样调查的学生人数为 ,图①中m的值是 ;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm)
160
165
170
175
180
学生人数(人)
1
3
2
2
2
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm
B.165cm,170cm
C.170cm,165cm
D.170cm,170cm -
科目: 来源: 题型:
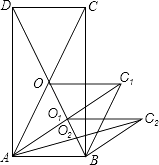
查看答案和解析>>【题目】如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )
A. cm2
cm2
B. cm2
cm2
C.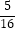 cm2
cm2
D. cm2
cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是外角和的3倍,则它是_________ 边形.
相关试题

