【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?(要有必要的过程)
参考答案:
【答案】
(1)解:如图1,由∠C=90°,AB=5cm,BC=3cm,
∴AC=4,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,
∴出发2秒后,则CP=2,
∵∠C=90°,
∴PB= ![]()
∴△ABP的周长为:AP+PB+AB=2+5+ ![]() =7+
=7+ ![]()
(2)解:①如图2,若P在边AC上时,BC=CP=3cm,
此时用的时间为3s,△BCP为等腰三角形;

②若P在AB边上时,有三种情况:
i)如图3,若使BP=CB=3cm,此时AP=2cm,P运动的路程为2+4=6cm,
所以用的时间为6s,△BCP为等腰三角形;
ii)如图4,若CP=BC=3cm,过C作斜边AB的高,根据面积法求得高为2.4cm,
作CD⊥AB于点D,
在Rt△PCD中,PD=1.8,
所以BP=2PD=3.6cm,
所以P运动的路程为9-3.6=5.4cm,
则用的时间为5.4s,△BCP为等腰三角形;
ⅲ)如图5,若BP=CP,此时P应该为斜边AB的中点,P运动的路程为4+2.5=6.5cm
则所用的时间为6.5s,△BCP为等腰三角形;
综上所述,当t为3s、5.4s、6s、6.5s时,△BCP为等腰三角形
【解析】(1)根据勾股定理求出AC的长,由出发2秒后,得到CP=2,再根据勾股定理求出PB的长,得到△ABP的周长;(2)①若P在边AC上时,BC=CP=3cm,此时用的时间为3s,△BCP为等腰三角形;②若P在AB边上时,有三种情况,若使BP=CB=3cm,此时AP=2cm,P运动的路程为2+4=6cm,所以用的时间为6s,△BCP为等腰三角形;若CP=BC=3cm,过C作斜边AB的高,根据面积法求得高为2.4cm,得到用的时间为5.4s,△BCP为等腰三角形;若BP=CP,此时P应该为斜边AB的中点,P运动的路程为4+2.5=6.5cm,所用的时间为6.5s,△BCP为等腰三角形;此题是综合题,难度较大,分类讨论时需认真仔细.
【考点精析】解答此题的关键在于理解等腰三角形的判定的相关知识,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过点A(﹣3,5)和点B(﹣3,2)作直线,则直线AB( )
A.平行于x轴
B.平行于y轴
C.与y轴相交
D.垂直于y轴 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发出一款新的节能产品,该产品的成本价位
 元/件,该产品在正式投放市场前通过代销点进行了为期一个月(
元/件,该产品在正式投放市场前通过代销点进行了为期一个月(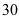 天)的试销售,售价为
天)的试销售,售价为 元/件.工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线
元/件.工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线 表示日销售量
表示日销售量 (件)与销售时间
(件)与销售时间 (天)之间的函数关系,已知线段
(天)之间的函数关系,已知线段 表示的函数关系中,时间每增加
表示的函数关系中,时间每增加 天,日销售量减少
天,日销售量减少 件.
件.
⑴第
 天的日销售量是 件,日销售利润是 元;
天的日销售量是 件,日销售利润是 元;⑵求
 与
与 之间的函数关系式,并写出
之间的函数关系式,并写出 的取值范围;
的取值范围;⑶日销售利润不低于
 元的天数共有多少天?试销售期间,日销售最大利润是多少元?
元的天数共有多少天?试销售期间,日销售最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(x,y)的坐标满足xy=0(x≠y),则点P必在( )
A.原点上
B.x轴上
C.y轴上
D.x轴上或y轴上(除原点) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.“任意画出一个等边三角形,它是轴对称图形”是随机事件
B.“任意画出一个平行四边形,它是中心对称图形”是必然事件
C.“概率为0.0001的事件”是不可能事件
D.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,以
,以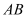 为直径的⊙
为直径的⊙ 与边
与边 分别交于
分别交于 两点,过点
两点,过点 作
作 ,垂足为点
,垂足为点 .
.
⑴求证:
 是⊙
是⊙ 的切线;
的切线;⑵若
 ,求
,求 的长
的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】联欢会上,A、B、C三名选手站在一个三角形三个顶点上玩抢凳子游戏,在他们中间放个木凳,谁先抢到凳子就获胜,为使游戏公平,凳子应放的最适当位置是△ABC的
A. 三边中线的交点 B. 三边中垂线的交点 C. 三条角平分线的交点 D. 三边上高的交点
相关试题

