Question

【题目】已知：如图，在△ABC、△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E三点在同一直线上，连接BD．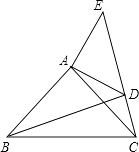

求证：
（1）△BAD≌△CAE；
（2）试猜想BD、CE有何特殊位置关系，并证明．

Answer 1

【答案】
（1）证明：∵∠BAC=∠DAE=90°

∴∠BAC+∠CAD=∠DAE+CAD

即∠BAD=∠CAE，

又∵AB=AC，AD=AE，

∴△BAD≌△CAE（SAS）

（2）证明：BD、CE特殊位置关系为BD⊥CE．

证明如下：由（1）知△BAD≌△CAE，

∴∠ADB=∠E．

∵∠DAE=90°，

∴∠E+∠ADE=90°．

∴∠ADB+∠ADE=90°．

即∠BDE=90°．

∴BD、CE特殊位置关系为BD⊥CE

【解析】要证（1）△BAD≌△CAE，现有AB=AC，AD=AE，需它们的夹角∠BAD=∠CAE，而由∠BAC=∠DAE=90°很易证得．（2）BD、CE有何特殊位置关系，从图形上可看出是垂直关系，可向这方面努力．要证BD⊥CE，需证∠BDE=90°，需证∠ADB+∠ADE=90°可由直角三角形提供．