【题目】在茶节期间，某茶商订购了甲种茶叶90吨，乙种茶叶80吨，准备用A、B两种型号的货车共20辆运往外地．已知A型货车每辆运费为0.4万元，B型货车每辆运费为0.6万元．（13分）

（1）设A型货车安排x辆，总运费为y万元，写出y与x的函数关系式；

（2）若一辆A型货车可装甲种茶叶6吨，乙种茶叶2吨；一辆B型货车可装甲种茶叶3吨，乙种茶叶7吨．按此要求安排A、B两种型号货车一次性运完这批茶叶，共有哪几种运输方案？

（3）说明哪种方案运费最少？最少运费是多少万元？

参考答案：

【答案】（1）y=﹣0.2x+12；(2) 三种运输方案：①A型货车10辆，B型货车10辆；②A型货车11辆，B型货车9辆；

③A型货车12辆，B型货车8辆．(3) 方案③运费最少，最少运费为9.6万元．

【解析】试题分析：（1）设A种货车为x辆，则B种货车为（20-x）辆，则表示出两种车的费用的和就是总费用，据此即可求解；

（2）仓库有甲种茶叶90吨，A型货车可装甲种茶叶6吨，乙种茶叶2吨；一辆B型货车可装甲种茶叶3吨，乙种茶叶7吨，据此即可得到一个关于x的不等式组，再根据x是整数，即可求得x的值，从而确定运输方案；

（3）运费可以表示为x的函数，根据函数的性质，即可求解．

试题解析：（1）设A种货车为x辆，则B种货车为（20-x）辆．

根据题意，得y=0.4x+0.6（20-x）=-0.2x+12；

（2）由题意得，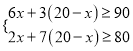

解得10≤x≤12．

又∵x为正整数，

∴x=10，11，12，

∴20-x=10，9，8．

∴有以下三种运输方案：

①A型货车10辆，B型货车10辆；

②A型货车11辆，B型货车9辆；

③A型货车12辆，B型货车8辆．

（3）∵方案①运费：10×0.4+10×0.6=10（万元）；

方案②运费：11×0.4+9×0.6=9.8（万元）；

方案③运费：12×0.4+8×0.6=9.6（万元）．

∴方案③运费最少，最少运费为9.6万元．

关闭