【题目】有一批共享单车需要维修,维修后继续投放骑用,现有甲、乙两人做维修,甲每天维修16辆,乙每天维修的车辆比甲多8辆,甲单独维修完成这批共享单车比乙单独维修完多用20天,公司每天付甲80元维修费,付乙120元维修费.
(1)问需要维修的这批共享单车共有多少辆?
(2)在维修过程中,公司要派一名人员进行质量监督,公司负担他每天10元补助费,现有三种维修方案:①由甲单独维修;
②由乙单独维修;
③甲、乙合作同时维修,你认为哪种方案最省钱,为什么?
参考答案:
【答案】(1)960辆;(2)方案三最省钱,理由见详解.
【解析】
(1)通过理解题意可知本题的等量关系,即甲乙单独修完共享单车的数量相同,列方程求解即可;
(2)分别计算,通过比较选择最省钱的方案.
解:(1)设乙单独做需要x天完成,则甲单独做需要(x+20)天,由题意可得:
16(x+20)=(16+8)x,
解得:x=40,
总数:(16+8)×40=960(辆),
∴这批共享单车一共有960辆;
(2)方案一:甲单独完成:60×80+60×10=5400(元),
方案二:乙单独完成:40×120+40×10=5200(元),
方案三:甲、乙合作完成:960÷(16+24)=24(天),
则一共需要:24×(120+80)+24×10=5040(元),
∵![]() ,
,
∴方案三最省钱.
-
科目: 来源: 题型:
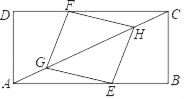
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,则反比例函数
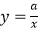 与一次函数y=bx+c在同一坐标系中的大致图象是( )
与一次函数y=bx+c在同一坐标系中的大致图象是( ) 
A.
B.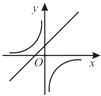
C.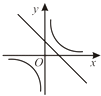
D.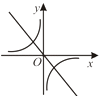
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂新开发生产一种机器,每台机器成本y(万元)与生产数量x(台)之间满足一次函数关系(其中10≤x≤70,且为整数),函数y与自变量x的部分对应值如表
x单位:台)
10
20
30
y(单位:万元/台)
60
55
50
(1)求y与x之间的函数关系式;
(2)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.
①该厂第一个月生产的这种机器40台都按同一售价全部售出,请求出该厂第一个月销售这种机器的总利润.(注:利润=售价﹣成本)
②若该厂每月生产的这种机器当月全部售出,则每个月生产多少台这种机器才能使每台机器的利润最大?
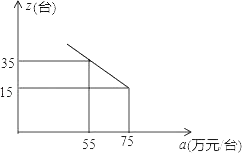
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在四边形ABCD中,点E、点F分别为AD、BC的中点,连接EF.
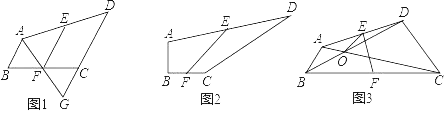
(1)如图1,AB∥CD,连接AF并延长交DC的延长线于点G,则AB、CD、EF之间的数量关系为 ;
(2)如图2,∠B=90°,∠C=150°,求AB、CD、EF之间的数量关系?
(3)如图3,∠ABC=∠BCD=45°,连接AC、BD交于点O,连接OE,若AB=
 ,CD=2
,CD=2 ,BC=6,则OE= .
,BC=6,则OE= . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A,B分别是x轴正半轴与y轴正半轴上一点,OA=m,OB=n,以AB为边在第一象限内作正方形ABCD.
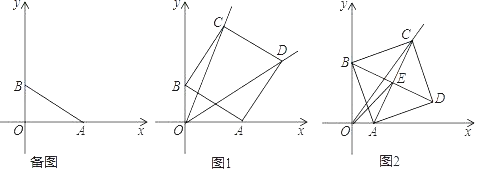
(1)若m=4,n=3,直接写出点C与点D的坐标;
(2)点C在直线y=kx(k>1且k为常数)上运动.
①如图1,若k=2,求直线OD的解析式;
②如图2,连接AC、BD交于点E,连接OE,若OE=2
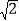 OA,求k的值.
OA,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=
 ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
相关试题

