【题目】顺次连接等腰梯形各边中点所成的四边形是
参考答案:
【答案】菱形
【解析】解:已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是各边的中点, 求证:四边形EFGH是菱形
证明:连接AC、BD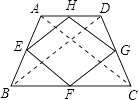
∵E、F分别是AB、BC的中点
∴EF= ![]() AC
AC
同理FG= ![]() BD,GH=
BD,GH= ![]() AC,EH=
AC,EH= ![]() BD
BD
又∵四边形ABCD是等腰梯形
∴AC=BD
∴EF=FG=GH=HE
∴四边形EFGH是菱形.
所以答案是:菱形.
【考点精析】认真审题,首先需要了解三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半),还要掌握菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法:
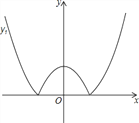
①当m=1,且y1与y2恰好有三个交点时b有唯一值为1;
②当b=2,且y1与y2恰有两个交点时,m>4或0<m<
 ;
; ③当m=-b时,y1与y2一定有交点;
④当m=b时,y1与y2至少有2个交点,且其中一个为(0,m).
其中正确说法的序号为 ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍,我们把这条对角线叫做这个四边形的黄金线,这个四边形叫做黄金四边形.

(1)如图1,在四边形ABCD中,AB=AD=DC,对角线AC,BD都是黄金线,且AB<AC,CD<BD,求四边形ABCD各个内角的度数;
(2)如图2,点B是弧AC的中点,请在⊙O上找出所有的点D,使四边形ABCD的对角线AC是黄金线(要求:保留作图痕迹);
(3)在黄金四边形ABCD中,AB=BC=CD,∠BAC=30°,求∠BAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y1=
 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.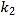
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式
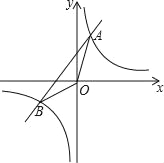 x+b的解.
x+b的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列第(1)题中的计算方法,再计算第(2)题中式子的值.
(1)﹣
 +(﹣9
+(﹣9 )+17
)+17 +(﹣3
+(﹣3 )
)解:原式=[(﹣5)+(﹣
 )]+[(﹣9)+(﹣
)]+[(﹣9)+(﹣ )]+[(+17)+(+
)]+[(+17)+(+ )]+[(﹣3)+(﹣
)]+[(﹣3)+(﹣ )]
)]=[(﹣5)+(﹣9)+(+17)+(﹣3)]+[(﹣
 )+(﹣
)+(﹣ )+(+
)+(+ )+(﹣
)+(﹣ )]
)]=0+(﹣1
 )
)=﹣1

上面这种方法叫拆项法.仿照上述方法计算:
(2)(﹣2008
 )+(﹣2007
)+(﹣2007 )+4017
)+4017 +(﹣1
+(﹣1 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边分别为3和7,则此三角形的第三边可能是( )
A. 3B. 4C. 6D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】延长线段AB到C,下列说法正确的是( )
A.点C在线段AB上
B.点C在直线AB上
C.点C不在直线AB上
D.点C在直线BA的延长线上
相关试题

