【题目】如图,在△ABC中,∠B=38°,∠C=112°.(1)按下列要求作图:(保留作图痕迹)
①BC边上的高AD;
②∠A的平分线AE.
(2)求∠DAE的度数.
参考答案:
【答案】①见解析;②见解析;(2) 37°.
【解析】
(1)①过点A作AD⊥BC即可;②作∠A的角平分线AE即可;(2)先根据三角形内角和定理求出∠BAC的度数,由角平分线的定义求出∠BAE的度数,再由直角三角形的性质可得出∠BAD的度数,进而可得出结论.
:(1)如图所示;
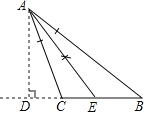
(2)在△ABC中,∠BAC=180°-112°-38°=30°,
∵AE平分∠BAC,∴∠BAE=![]() ∠BAC=15°,
∠BAC=15°,
在Rt△ADB中,∠BAD=90°-∠B=52°,
∴∠DAE=∠DAB-∠BAE=37°.
-
科目: 来源: 题型:
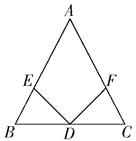
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.你添加的条件是 .(不再添加辅助线和字母)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=72°30′,射线OC在∠AOB内,∠BOC=30°,
(1)∠AOC=_______;
(2)在图中画出∠AOC的一个余角,要求这个余角以O为顶点,以∠AOC的一边为边.图中你所画出的∠AOC的余角是______,这个余角的度数等于______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面四个整式中,不能表示图中阴影部分面积的是( )

A. (x+3)(x+2)﹣2x B. x(x+3)+6 C. 3(x+2)+x2 D. x2+5x
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空,完成下列说理过程:
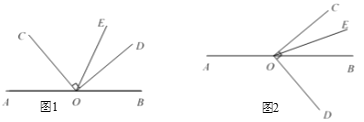
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;
解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =
 ∠BOC ( ).
∠BOC ( ).∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上A点表示数0,B点表示的数是最小的正整数,C点表示数5,点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.

(1) BC= .
(2) A,B,C在数轴上同时运动,点B和点C分别以每秒3个单位长度和6个单位长度的速度向右运动,点A以每秒a个单位长度的速度向左运动。在运动过程中,3BC-2AB的值始终保持不变,请求出a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,某超市从一楼到二楼有一自动扶梯,图②是侧面示意图.已知自动扶梯AB的坡度为1∶2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ , C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN , 在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )

A.10.8米
B.8.9米
C.8.0米
D.5.8米
相关试题

