【题目】已知关于![]() 的方程
的方程![]() 有两个实数根
有两个实数根![]() 、
、![]() .
.
(1)求实数k的取值范围;
(2)若![]() 、
、![]() 满足
满足![]() ,求实数
,求实数![]() 的值.
的值.
参考答案:
【答案】(1)k≤![]() ;(2)﹣2.
;(2)﹣2.
【解析】试题分析:(1)根据方程的系数结合根的判别式,即可得出△=-4k+5≥0,解之即可得出实数k的取值范围;
(2)由根与系数的关系可得x1+x2=1-2k、x1x2=-1,将其代入x12+x22=(x1+x2)2-2x1x2=16+x1x2中,解之即可得出k的值.
试题解析:(1)∵关于x的方程x2+(2k﹣1)x+k2﹣1=0有两个实数根x1,x2,
∴△=(2k﹣1)2﹣4(k2﹣1)=﹣4k+5≥0,
解得:k≤![]() ,
,
∴实数k的取值范围为k≤![]() ;
;
(2)∵关于x的方程x2+(2k﹣1)x+k2﹣1=0有两个实数根x1,x2,
∴x1+x2=1﹣2k,x1x2=k2﹣1,
∵x12+x22=(x1+x2)2﹣2x1x2=16+x1x2,
∴(1﹣2k)2﹣2×(k2﹣1)=16+(k2﹣1),即k2﹣4k﹣12=0,
解得:k=﹣2或k=6(不符合题意,舍去),
∴实数k的值为﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如下表:

根据上表中的信息判断,下列结论中错误的是( )
A. 该班一共有40名同学 B. 该班学生这次考试成绩的众数是28分
C. 该班学生这次考试成绩的中位数是28分 D. 该班学生这次考试成绩的平均数是28分
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动.学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:


请根据图表信息回答下列问题:
(1)频数分布表中的
 ,
, ;
;(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在
 小时以上的学生评为“阅读之星”,请你估计该校
小时以上的学生评为“阅读之星”,请你估计该校 名学生中评为“阅读之星”的有多少人?
名学生中评为“阅读之星”的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据:
 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数1至2019按照一定规律排成下表:

记aij表示第i行第j个数,如a14=4表示第1行第4个数是4.
(1)直接写出a42= ,a53= ;
(2)①如果aij=2019,那么i= ,j= ;②用i,j表示aij= ;
(3)将表格中的5个阴影格子看成一个整体并平移,所覆盖的5个数之和能否等于2027.若能,求出这5个数中的最小数,若不能说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O为数轴原点,点A在数轴上对应的数为a,点B对应的数为b,A、B之间的距离记作AB,且|a+4|+(b﹣10)2=0.

(1)求线段AB的长;
(2)设点P在数轴上对应的数为x,当PA+PB=20时,求x的值;
(3)如图,M、N两点分别从O、B出发以v1、v2的速度同时沿数轴负方向运动(M在线段AO上,N在线段BO上),P是线段AN的中点,若M、N运动到任一时刻时,总有PM为定值,下列结论:①
 的值不变;②v1+v2的值不变.其中只有一个结论是正确的,请你找出正确的结论并求值.
的值不变;②v1+v2的值不变.其中只有一个结论是正确的,请你找出正确的结论并求值. -
科目: 来源: 题型:
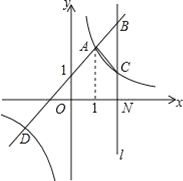
查看答案和解析>>【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=
 (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
相关试题

