【题目】已知:如图,A、B、C、D 为矩形的四个顶点,AB=16cm,AD=
6cm,动点P、Q 分别从A、C 同时出发,点P 以3cm/s的速度向点B 移动,
一直到达点 B 为止,点 Q 以2cm/s的速度向点 D 移动.
(1)P、Q 两点从出发点出发几秒时,四边形PBCQ 的面积是33cm2?
(2)P、Q 两点从出发点出发几秒时,点P、Q 间的距离是10cm?

参考答案:
【答案】(1)P、Q 两点出发5秒时,四边形PBCQ 的面积为33cm2.
(2) P、Q 两点从出发点出发![]() 秒或
秒或![]() 秒时,点P 与点Q 的距离是10cm.
秒时,点P 与点Q 的距离是10cm.
【解析】解:(1)设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2,
则PB=(16﹣3x)cm,QC=2xcm,
根据梯形的面积公式得![]() (16﹣3x+2x)×6=33,
(16﹣3x+2x)×6=33,
解之得x=5,
(2)设P,Q两点从出发经过t秒时,点P,Q间的距离是10cm,
作QE⊥AB,垂足为E,
则QE=AD=6,PQ=10,
∵PA=3t,CQ=BE=2t,
∴PE=AB﹣AP﹣BE=|16﹣5t|,
由勾股定理,得(16﹣5t)2+62=102,
解得t1=4.8,t2=1.6.
答:(1)P、Q两点从出发开始到5秒时四边形PBCQ的面积为33cm2;
(2)从出发到1.6秒或4.8秒时,点P和点Q的距离是10cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx-3(a≠0)的图象经过点(1,3),则代数式1-a-b的值为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=
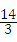 米时,有DC2=AE2+BC2.
米时,有DC2=AE2+BC2.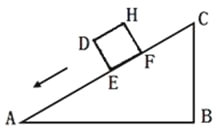
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知二次函数
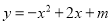 .
.(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点(﹣2,5),并且与y轴交于点P,直线y=
 x+3与y轴交于点Q,点Q恰与点P关于x轴对称,求这个一次函数的解析式.
x+3与y轴交于点Q,点Q恰与点P关于x轴对称,求这个一次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】“割圆术”是求圆周率的一种算法,公元263年左右,我国一位著名的数学家发现当圆的内接正多边形的边数无限增加时,多边形面积可无限逼近圆面积,即所谓“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”. 请问上述著名数学家为 ( )
A.刘徽B.祖冲之C.杨辉D.赵爽
相关试题

