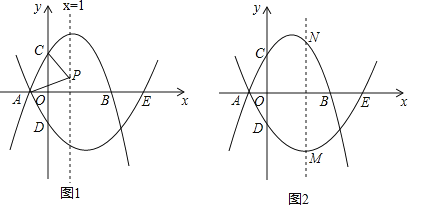
【题目】已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣ ![]() ).
).
(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.
参考答案:
【答案】(1)y=![]() x2﹣2x﹣
x2﹣2x﹣![]() ;(2)(1,1);(3)12.
;(2)(1,1);(3)12.
【解析】试题分析:(1)由对称轴可求得b,可求得l1的解析式,令y=0可求得A点坐标,再利用待定系数法可求得l2的表达式;(2)设P点坐标为(1,y),由勾股定理可表示出PC2和PA2,由条件可得到关于y的方程可求得y,可求得P点坐标;(3)可分别设出M、N的坐标,可表示出MN,再根据函数的性质可求得MN的最大值.
试题解析:(1)∵抛物线l1:y=﹣x2+bx+3的对称轴为x=1, ∴﹣![]() =1,解得b=2,
=1,解得b=2,
∴抛物线l1的解析式为y=﹣x2+2x+3, 令y=0,可得﹣x2+2x+3=0,解得x=﹣1或x=3,
∴A点坐标为(﹣1,0),
∵抛物线l2经过点A、E两点, ∴可设抛物线l2解析式为y=a(x+1)(x﹣5),
又∵抛物线l2交y轴于点D(0,﹣![]() ), ∴﹣
), ∴﹣![]() =﹣5a,解得a=
=﹣5a,解得a=![]() , ∴y=
, ∴y=![]() (x+1)(x﹣5)=
(x+1)(x﹣5)=![]() x2﹣2x﹣
x2﹣2x﹣![]() ,
,
∴抛物线l2的函数表达式为y=![]() x2﹣2x﹣
x2﹣2x﹣![]() ;
;
(2)设P点坐标为(1,y),由(1)可得C点坐标为(0,3),
∴PC2=12+(y﹣3)2=y2﹣6y+10,PA2=[1﹣(﹣1)]2+y2=y2+4, ∵PC=PA,
∴y2﹣6y+10=y2+4,解得y=1, ∴P点坐标为(1,1);
(3)由题意可设M(x,![]() x2﹣2x﹣
x2﹣2x﹣![]() ), ∵MN∥y轴, ∴N(x,﹣x2+2x+3),
), ∵MN∥y轴, ∴N(x,﹣x2+2x+3),![]() x2﹣2x﹣
x2﹣2x﹣![]()
令﹣x2+2x+3=![]() x2﹣2x﹣
x2﹣2x﹣![]() ,可解得x=﹣1或x=
,可解得x=﹣1或x=![]() ,
,
①当﹣1<x≤![]() 时,MN=(﹣x2+2x+3)﹣(
时,MN=(﹣x2+2x+3)﹣(![]() x2﹣2x﹣
x2﹣2x﹣![]() )=﹣
)=﹣![]() x2+4x+
x2+4x+![]() =﹣
=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
显然﹣1<![]() ≤
≤![]() ,∴当x=
,∴当x=![]() 时,MN有最大值
时,MN有最大值![]() ;
;
②当![]() <x≤5时,MN=(
<x≤5时,MN=(![]() x2﹣2x﹣
x2﹣2x﹣![]() )﹣(﹣x2+2x+3)=
)﹣(﹣x2+2x+3)=![]() x2﹣4x﹣
x2﹣4x﹣![]() =
=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
显然当x>![]() 时,MN随x的增大而增大,
时,MN随x的增大而增大,
∴当x=5时,MN有最大值,![]() ×(5﹣
×(5﹣![]() )2﹣
)2﹣![]() =12;
=12;
综上可知在点M自点A运动至点E的过程中,线段MN长度的最大值为12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:

并求得了A产品三次单价的平均数和方差:
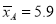 ;
; 
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的平均数和方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,若B产品第四次调价后为m元(3<m<4),此时B产品四次单价的中位数是A产品这四次单价的中位数的
 倍,求m.
倍,求m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式由左边到右边的变形中,属于因式分解的是( )
A.(a﹣2)(a+2)=a2﹣4
B.8x2y=8×x2y
C.m2﹣1+n2=(m+1)(m﹣1)+n2
D.x2+2x﹣3=(x﹣1)(x+3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ΔABC内接于⊙O,D是⊙O上一点,连结BD、CD,AC、BD交于点E.
(1)请找出图中的相似三角形,并加以证明(不添加其他线条的情况下);
(2)若∠D=45°,BC=4,求⊙O的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边分别是5和10,则第三边长x的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水库的水位在5小时内持续上涨,初始水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y(米)与时间x(小时)(0≤x≤5)的函数关系式为 .
相关试题

